Binary Search Algorithm

What is Binary Search?

Binary Search Algorithm is one of the widely used searching techniques. It can be used to sort arrays. This searching technique follows the divide and conquer strategy. The search space always reduces to half in every iteration.

Binary Search Algorithm is a very efficient technique for searching but it needs some order on which partition of the array will occur.

Advantages of Binary Search Algorithm

Since it follows the technique to eliminate half of the array elements, it is more efficient as compared to linear search for large data.
Better time complexity and thus takes less compilation time.
An improvement over linear search as it breaks the array down in half rather than sequentially traversing through the array elements.

Limitations of Binary Search Algorithm

Binary Search algorithm could only be implemented over a sorted array.
Small unsorted arrays would take considerate time in sorting and then searching the desired element. So, binary search is not preferred in such cases.
It has poor locality of reference compared to linear search algorithm when comes to in-memory searching for short intervals.

Applications of Binary Search

This algorithm is used to search element in a given sorted array with more efficiency.
It could also be used for few other additional operations like- to find the smallest element in the array or to find the largest element in the array.

Binary Search Pseudocode

We are given an input array that is supposed to be sorted in ascending order.
We take two variables which will act as a pointer i.e, beg, and end.
Beg will be assigned with 0 and the end will be assigned to the last index of the array.
Now we will introduce another variable mid which will mark the middle of the current array. That will be computed as (low+high)/2.
If the element present at the mid index is equal to the element to be searched, then just return the mid index.
If the element to be searched is smaller than the element present at the mid index, move end to mid-1, and all RHS will get discarded.
If the element to be searched is greater than the element present at the mid index, move beg to mid+1, and all LHS will get discarded.

Iterative approach

binarySearch(arr, size)
		   loop until beg is not equal to end
    midIndex = (beg + end)/2
    if (item == arr[midIndex] )
        return midIndex
    else if (item > arr[midIndex] ) 
        beg = midIndex + 1
    else                       
        end = midIndex - 1

Recursive approach

binarySearch(arr, item, beg, end)
    if beg<=end
        midIndex = (beg + end) / 2 
        if item == arr[midIndex]
            return midIndex
        else if item < arr[midIndex]        
            return binarySearch(arr, item, midIndex + 1, end)
        else                              
            return binarySearch(arr, item, beg, midIndex - 1)
    
    return -1

Binary Search Algorithm Dry Run

Item to be searched=20

input:

0	1	2	3	4
10	11	16	20	23

beg=0, end=4, mid=2

0	1	2	3	4
10	11	16	20	23

beg=3, end=4, mid=3

0	1	2	3	4
10	11	16	20	23

Element found at index 3, Hence 3 will get returned.

2. Given is the pictorial representation of binary search through an array of size 6 arranged in ascending order. We intend to search the element 78:

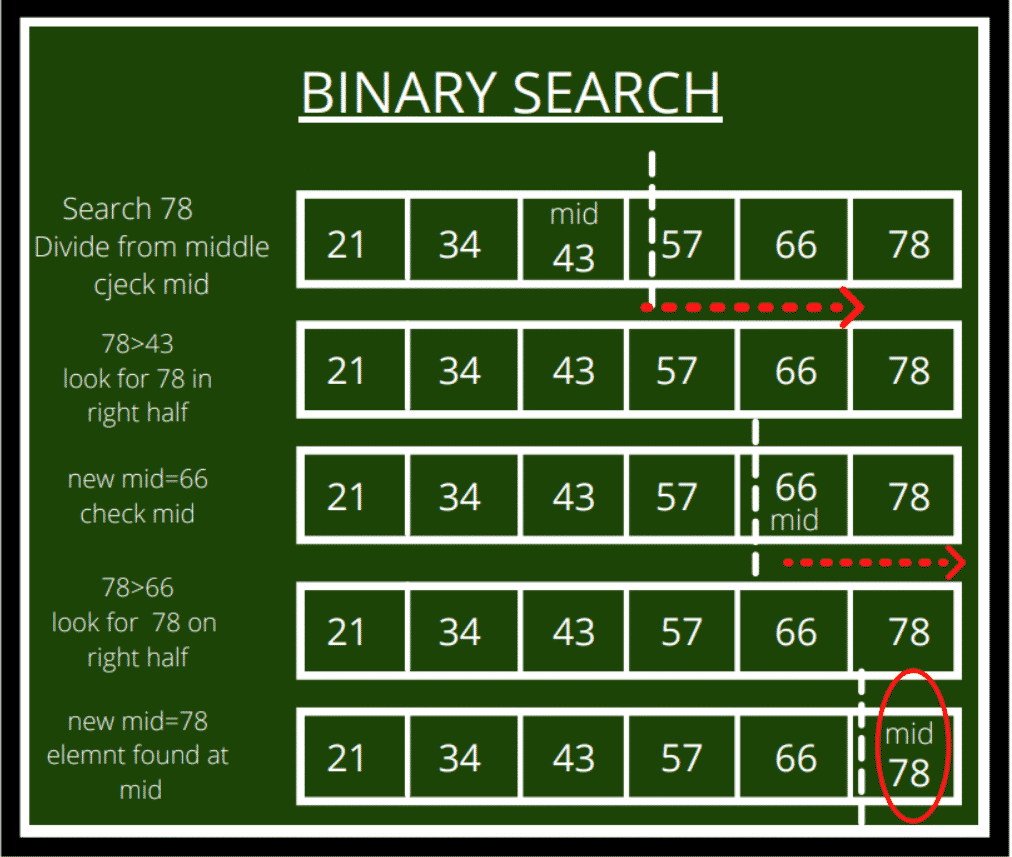
Binary Search Time Complexity

In each iteration, the search space is getting divided by 2. That means that in the current iteration you have to deal with half of the previous iteration array.
And the above steps continue till beg<end
Best case could be the case where the first mid-value get matched to the element to be searched
Best Time Complexity: O(1)
Average Time Complexity: O(logn)
Worst Time Complexity: O(logn)

Calculating Time complexity of binary search

Let k be the number of iterations.

(E.g. If a binary search gets terminated after four iterations, then k=4.)

In a binary search algorithm, the array taken gets divided by half at every iteration.
If n is the length of the array at the first iteration, then at the second iteration, the length of the array will be n/2
Again dividing by half in the third iteration will make the array’s length = (n/2)/2=n/(2^k).
Similarly, at the fourth iteration, the value of the array’s length will be n/(2^3). and so on.
At the kth iteration, the value of the length of the array will be = (n/2^k).

As after k divisions, the length of the array becomes 1 therefore,

n/(2^k)=1

=> n = 2k

Applying log function on both sides:

=>log(n) = log (2^k) (log with base 2)

=>log (n) = k log (2) (log with base 2)

As (log (a) = 1) (log with base 2)

Therefore,

=> k = log (base 2) (n)

Therefore, the time complexity of the Binary Search algorithm is log (base 2) n.

Binary Search Space Complexity

No auxiliary space is required in Binary Search implementation

The binary search algorithm’s space complexity depends on the way the algorithm has been implemented. Two ways in which it can be implemented are:

Iterative method: In this method, the iterations are controlled through looping conditions. The space complexity of binary search in the iterative method is O(1).

Recursive method: In this method, there is no loop, and the new values are passed to the next recursion of the loop. Here, the max and min values are used as the boundary condition. The space complexity of binary search in the recursive method is O(log n).

Binary Search in C

Iterative Binary Search in C

Code:

#include <stdio.h>
int binarySearch( int arr[], int item, int beg, int end) {
  while (beg <= end) {
    int midIndex = beg + (end - beg) / 2;
    if (arr[midIndex] == item)
      return midIndex;
    if (arr[midIndex] > item)
      beg = midIndex + 1;
    else
      end = midIndex - 1;
  }
  return -1;
}
int main(void) {
  int arr[] = {13, 45, 65, 16, 117, 82, 19};
  int n = sizeof(arr) / sizeof(arr[0]);
  int item = 45;
  int ans = binarySearch(arr, item, 0, n - 1);
  if (ans == -1)
    printf("Element not present");
  else
    printf("answer: %d", ans);
  return 0;
}

Output:

answer: 1

Recursive Binary Search in C

Code:

#include <stdio.h>
int binarySearch(int arr[], int item, int beg, int end) {
  if (end >= beg) {
    int midIndex = beg + (end - beg) / 2;
    if (arr[midIndex] == item)
      return midIndex;
    if (arr[midIndex] < item)
      return binarySearch(arr, item, beg, midIndex - 1);
    return binarySearch(arr, item, midIndex + 1, end);
  }
  return -1;
}
int main(void) {
  int arr[] = {13, 45, 65, 16, 117, 82, 19};
  int n = sizeof(arr) / sizeof(arr[0]);
  int item = 45;
  int ans = binarySearch(arr, item, 0, n - 1);
  if (ans == -1)
    printf("Element not present");
  else
    printf("answer: %d", ans);
  return 0;
}

Output:

answer: 1

Binary Search in JAVA

Iterative Binary Search in JAVA

Code:

class BinarySearch {
  int binarySearch(int arr[], int item, int beg, int end) {
    while (beg <= end) {
      int midIndex = beg + (end - beg) / 2;
      if (arr[midIndex] == item)
        return midIndex;
      if (arr[midIndex] > item)
        beg = midIndex + 1;
      else
        end = midIndex - 1;
    }
    return -1;
  }

  public static void main(String args[]) {
    BinarySearch ob = new BinarySearch();
    int arr[] = {13, 45, 65, 16, 117, 82, 19};
    int n = arr.length;
    int item = 45;
    int ans = ob.binarySearch(arr, item, 0, n - 1);
    if (ans == -1)
      System.out.println("Element not present");
    else
      System.out.println("answer: "+ans);
  }
}

Output:
answer: 1

Recursive Binary Search in JAVA

Code:

class BinarySearch {
    int binarySearch(int arr[], int item, int beg, int end) {
    if (end >= beg) {
      int midIndex = beg + (end - beg) / 2;
      if (arr[midIndex] == item)
        return midIndex;
      if (arr[midIndex] < item)
        return binarySearch(arr, item, beg, midIndex - 1);
      return binarySearch(arr, item, midIndex + 1, end);
    }
    return -1;
  }

  public static void main(String args[]) {
    BinarySearch ob = new BinarySearch();
    int arr[] = {13, 45, 65, 16, 117, 82, 19};
    int n = arr.length;
    int item = 45;
    int ans = ob.binarySearch(arr, item, 0, n - 1);
    if (ans == -1)
      System.out.println("Element not present");
    else
      System.out.println("answer: "+ans);
  }
}

Output:
answer: 1

Binary Search in C++

Iterative Binary Search in C++

Code:

#include <iostream>
using namespace std;
int binarySearch(int arr[], int item, int beg, int end) {
  while (beg <= end) {
    int midIndex = beg + (end - beg) / 2;
    if (arr[midIndex] == item)
      return midIndex;
    if (arr[midIndex] > item)
      beg = midIndex + 1;
    else
      end = midIndex - 1;
  }
  return -1;
}

int main(void) {
  int arr[] = {13, 45, 65, 16, 117, 82, 19};
  int n = sizeof(arr) / sizeof(arr[0]);
  int item = 45;
  int ans = binarySearch(arr, item, 0, n - 1);
  if (ans == -1)
    printf("Element not present");
  else
    printf("answer: %d", ans);
}

Output:
answer: 1

Recursive Binary Search in C++

Code:

#include <iostream>
using namespace std;

int binarySearch(int array[], int item, int beg, int end) {
  if (end >= beg) {
    int midIndex = beg + (end - beg) / 2;

    if (array[midIndex] == item)
      return midIndex;

    if (array[midIndex] < item)
      return binarySearch(array, item, beg, midIndex - 1);

    return binarySearch(array, item, midIndex + 1, end);
  }

  return -1;
}

int main(void) {
  int arr[] = {13, 45, 65, 16, 117, 82, 19};
  int n = sizeof(arr) / sizeof(arr[0]);
  int item = 45;
  int ans = binarySearch(arr, item, 0, n - 1);
  if (ans == -1)
    printf("Element not present");
  else
    printf("answer: %d", ans);
}

Output:
answer: 1

Binary Search in Python

Iterative Binary Search in Python

Code:

def binarySearch(arr, item, beg, end):
    while beg <= end:
        mid = beg + (end - beg)//2
        if arr[mid] == item:
            return mid
        elif arr[mid] > item:
            beg = mid + 1
        else:
            end = mid - 1
    return -1

arr = [13, 45, 65, 16, 117, 82, 19]
item = 45

ans = binarySearch(arr, item, 0, len(arr)-1)

if ans != -1:
    print("answer: " + str(ans))
else:
    print("Element not present")

Output:
answer: 1

Recursive Binary Search in Python

Code:

def binarySearch(arr, item, beg, end):
    if end >= beg:
        midIndex = beg + (end - beg)//2
        if arr[midIndex] == item:
            return midIndex
        elif arr[midIndex] < item:
            return binarySearch(arr, item, beg, midIndex-1)
        else:
            return binarySearch(arr, item, midIndex + 1, end)
    else:
        return -1

arr = [13, 45, 65, 16, 117, 82, 19]
item = 45

ans = binarySearch(arr, item, 0, len(arr)-1)

if ans != -1:
    print("answer: " + str(ans))
else:
    print("Element not present")

Output:
answer: 1

Binary Search Example

Example1:

Your task is to find the first and last occurrence of the given element in the array. If an element is not present, return -1. Assuming sorting here is in ascending order.

Example:

Input

1 2 5 5 5 5 6

Output

2 5

Code in Java:

import java.util.*;

class Demo {
	public static void main ( String[] args ) {
		    Scanner sc = new Scanner( System.in );
		    int n = sc.nextInt();
		    int[] arr = new int[n];
		    for( int i = 0 ; i < n ; i++ )
		    {
		        arr[i] = sc.nextInt();
		    }
		    int item = sc.nextInt();
		    int beg = 0, end = 0;
		    for( int i = 0 ; i < n ; i++ )
		    {
		        if( arr[i] == item )
		        {
		            beg = i;
		            break;
		        }
		        else{
		            beg = -1;
		        }
		    }
		    for( int i = arr.length - 1 ; i > 0; i-- )
		    {
		        if( arr[i] == item )
		        {
		            end = i;
		            break;
		        }
		    }
		    if(beg == -1)
		    {
		        System.out.println( -1 );
		    }
		    else {
		        System.out.println( beg + " " + end );
		    }	    
	}
}

Code in C++:

#include <iostream>
using namespace std;


int main(void) {
           
            int n;
            cin>>n;
            int arr[n];
            for( int i = 0 ; i < n; i++)
              cin>>arr[i];
            
            int item;
            cin>>item;
            int beg = 0, end = 0;
		    for( int i = 0 ; i < n ; i++ )
		    {
		        if( arr[i] == item )
		        {
		            beg = i;
		            break;
		        }
		        else{
		            beg = -1;
		        }
		    }
		    for( int i = n - 1 ; i > 0; i-- )
		    {
		        if( arr[i] == item )
		        {
		            end = i;
		            break;
		        }
		    }
		    if(beg == -1)
		    {
		        cout<<"-1";
		    }
		    else {
		        cout<<beg<<" "<<end;
		    }	
}

Code in C:

#include <stdio.h>

int main() {
            int n;
            scanf("%d ", &n);
            int arr[n];
            for( int i = 0 ; i < n; i++)
              scanf("%d ",&arr[i]);
            
            int item;
            scanf("%d ",&item);
            int beg = 0, end = 0;
		    for( int i = 0 ; i < n ; i++ )
		    {
		        if( arr[i] == item )
		        {
		            beg = i;
		            break;
		        }
		        else{
		            beg = -1;
		        }
		    }
		    for( int i = n - 1 ; i > 0; i-- )
		    {
		        if( arr[i] == item )
		        {
		            end = i;
		            break;
		        }
		    }
		    if(beg == -1)
		    {
		        printf("%d ",-1);
		    }
		    else {
		        printf("%d %d",beg,end);
		    }
}

Complexity of Searching, Insertion and Deletion in Binary Tree

A tree is binary when a node can have at most two children.

Let’s define the complexity of searching, insertion & deletion in a binary tree with an example.

E.g. The figure given below is a binary tree.

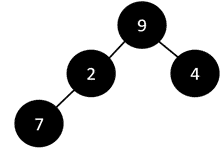
If we have to search for element 7, we will have to traverse all the elements to reach that element, therefore to perform searching in a binary tree, the worst-case complexity= O(n).

If we have to insert an element as the left child of element 7, we will have to traverse all the elements, therefore performing insertion in a binary tree, the worst-case complexity= O(n).

If we have to delete element 7, we will have to traverse all the elements to find it, therefore performing deletion in a binary tree, the worst-case complexity= O(n).

Complexity of Searching, Insertion and Deletion in Binary Search Tree (BST)

Binary Search Tree (BST) is considered as a special type of binary tree where the values are arranged in the following order: left child < parent node < right child.

Let’s define the complexity of searching, insertion & deletion in a binary search tree with an example.

E.g. The figure given below is a binary search tree.

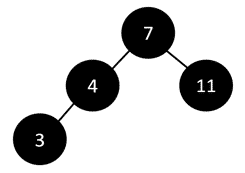
If we have to search for element 3, will have to traverse all the elements to reach that element, therefore to perform searching in a binary search tree, the worst-case complexity= O(n). In general, the time complexity is O(h) where h = height of binary search tree.

If we have to insert an element 2, we will have to traverse all the elements to insert it as the left child of 3. Therefore, to perform insertion in a binary search tree, the worst-case complexity= O(n) whereas the time complexity in general = O(h).

Suppose we have to delete the element 3. In that case, we will have to traverse all the elements to find it, therefore performing deletion in a binary tree, the worst-case complexity= O(n) whereas the time complexity in general = O(h).

Complexity of Searching, Insertion and Deletion in AVL Tree

AVL(Adelson-Velskii and Landis) tree is a binary search tree which is also known as height balanced tree as it has a property in which the difference between the height of the left sub-tree and the right sub-tree can never be more than 1.

Let’s define the complexity of searching, insertion & deletion in AVL tree with an example.

E.g. The figure given below is an AVL tree.

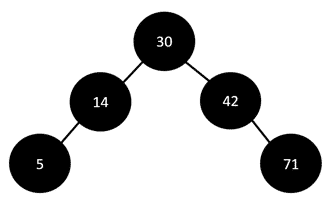
If we have to search for element 5, will have to traverse all the elements to reach that element i.e. in the order 30,14,5 = 3 = log n , therefore to perform searching in an AVL tree, the worst-case complexity= O(log n).

If we have to insert an element 92, we will have to traverse all the elements in order 30, 42, 71 to insert it as the right child of 71. Therefore, to perform insertion in an AVL tree, the worst-case complexity= O(log n).

If we have to delete the element 71, we will have to traverse all the elements to find it in the order 30, 42, 71. Therefore to perform deletion in an AVL tree, the worst-case complexity= O(log n).

Big O for Binary Search

Big O notation shows the number of operations that an algorithm will perform. It finds the upper bound that gives the worst-case running time complexity. It helps you understand how fast an algorithm is growing and allows you to compare the growth with others.

When the number of steps are counted, you divide the range into half and then process it. This process stops once both the upper and the lower bounds cross. This way you check the entry every time as you have half of the number of entries to check each time. Putting this into a formula as a recurrence T(n) we get:

T(n)=T(n/2)+1 (Binary search recurrence relation)

With base case T(1)=1.

By applying any variant of the Master Theorem, you get

T(n) ∈ O(log (n))

Running Time of Binary Search

Binary search halves the size of portion that is reasonable after every incorrect guess. If binary search makes a wrong guess, the portion of the array that contains reasonable guesses is reduced to half. For eg. if the portion had 40 elements then the incorrect guess comes down to 20.

If we start performing binary search on an array of 16 elements then the incorrect guessed will be reduced to length 8, then 4, then 2 and then 1. No more guesses occur once the reasonable portion comes down to just 1. 1 portion element can either be correct or incorrect and we have reached our result. So, for an array of length 16 elements, binary search requires five guesses at most.

Similarly for 32 elements, binary search will require at most 6 guesses to get the answer. We can see a pattern being formed here i.e., we require one more guess to get the result if the number of elements is doubled.

Let there be m number of guesses for an array of length n, then for an array of length 2n, the length cut down after the 1st guess will be n. Now, the number of guesses will become m+1.

(Taking up the general case of an array of length n, we can say that the number of time we are repeatedly reducing the length of n to half until we reach the value 1, plus one. We can write this mathematically with the base-2 logarithm of n.)

The worst case in binary search is achieved when the integers are equal which can be significant when the encoding lengths are large, like large integer types or long strings. This would make the comparison between elements expensive, also comparing the floating-point values are often more expensive than the comparison done between integers or short strings.

RB Tree

RB Tree (Red Black Tree) is a self-balancing binary search tree where left child < parent < right child. Each node in the RB tree is either red or black in color. These colors ensure that the tree maintains its balance when insertion or deletion of nodes is performed.

Properties:

Color of the root node is always black.
Parent node of red color does not contain a red child.
Every leaf node/NIL is of black color.
The descendent path from every node have the same black height. (Black Height Rule)

Time Complexity of RB Tree

For searching, the time complexity is O(log n).

For insertion, the time complexity is O(log n).

For deletion, the time complexity is O(log n).

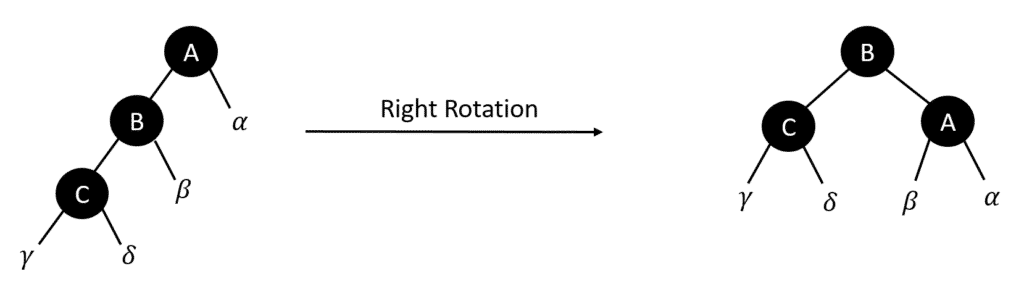
Rotation Operation on RB Tree

LR (Left Right) Rotation

RR (Right Right) Rotation

Insertion in RB Tree

Algorithm:

RB-INSERT (T, z)
 1. y ← nil [T]
 2. x ← root [T]
 3. while x ≠ NIL [T]
 4. do y ← x
 5. if key [z] < key [x]
 6. then x  ← left [x]
 7. else x ←  right [x]
 8. p [z] ← y
 9. if y = nil [T]
 10. then root [T] ← z
 11. else if key [z] < key [y]
 12. then left [y] ← z
 13. else right [y] ← z
 14. left [z] ← nil [T]
 15. right [z] ← nil [T]
 16. color [z] ← RED
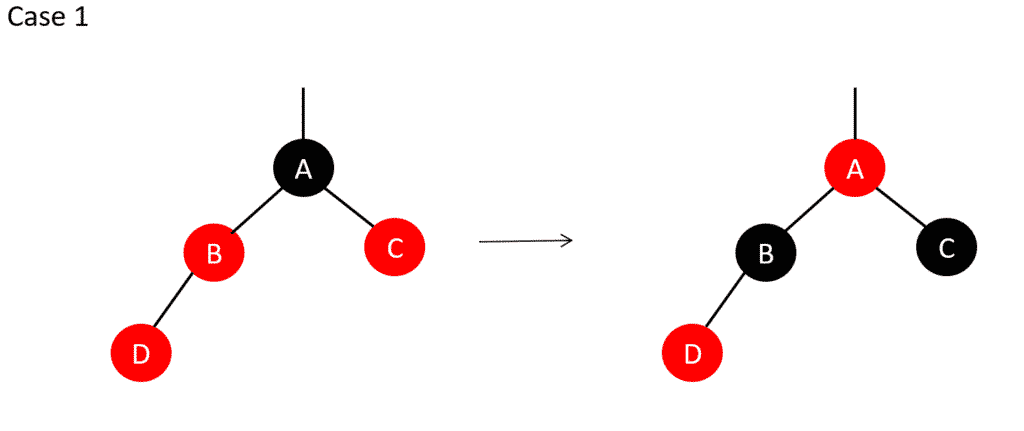
 17. RB-INSERT-FIXUP (T, z)

After inserting a node in RB Tree, the color of the nodes are fixed using the following algorithm to maintain the balance of the tree.

RB_INSERT_FIXUP(T,z)
1. While color [p[z]] = RED
2.   Do if p[z] = left [p[p[z]]
3.     then y ← right [p[p[z]]]
4.       if color [y] = RED
5.         then color [p[z]] ← BLACK      //Case 1
6.           color [y] ← BLACK            //Case 1
7.           color [p[p[z]]] ← RED        //Case 1
8.	     Z ← p[p[z]]                  //Case 1
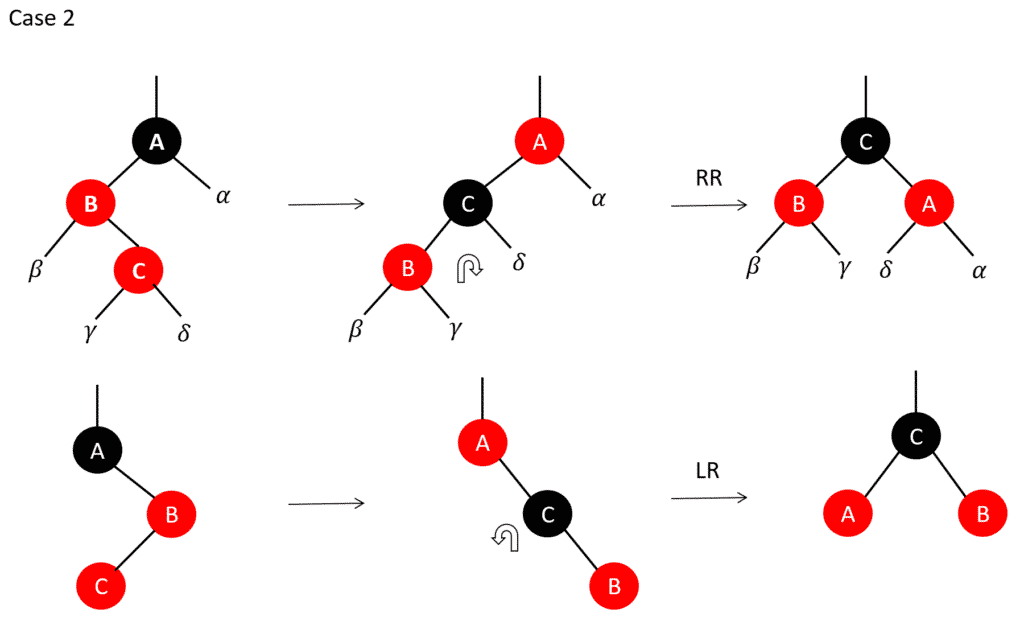
9.	 else if z = right [p[z]]
10.	   then z ← p[z]                  //Case 2
11.	     LEFT_ROTATE(T,z)             //Case 2
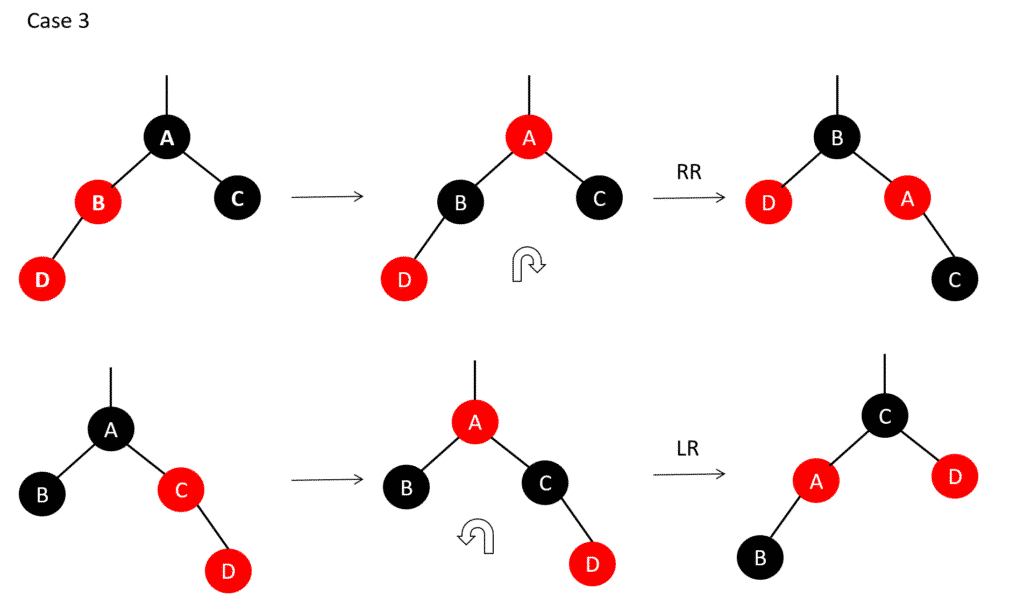
12.	   color [p[z]] ← BLACK           //Case 3
13.	   color [p[z]] ← RED             //Case 3
14.	   RIGHT_ROTATE(T,p[p[z]])        //Case 3
15.	 else (same as then clause with “right” & “left” exchange)
16. color [root[T]] ←  BLACK

Difference between Binary Tree and Binary Search Tree

Binary Tree	Binary Search Tree
A non-linear data structure having at most two child nodes.	A node based binary tree where the further subtrees are also binary search tree
It is unordered.	It is ordered.
Slower in the process of searching, insertion and deletion.	Faster in the process of searching, insertion and deletion.
No ordering is there in terms of how the nodes will be arranged.	The elements of the left subtree has values lesser than that of the right sub tree.

This brings us to the end of the blog on Binary Search Algorithm. We hope that you enjoyed it and were able to learn the concept of Binary Search Algorithm well. If you wish to upskill, you can check out Great Learning Academy’s Free online courses!