Time Value of Money

A bird in the hand is worth two in the bush one of the most popular proverbs you might ever hear in various contexts. Of course, this is one of the oldest adages yet highly relevant in the context of money.

Time value of money is one of the core principles in finance.

Trust me! You already know what the time value of money is. Let me take an example to prove that.

Of course! We all know what the time value of money is. We do use this principle in our daily lives but not sure how? Isn’t it? Let’s try it out.

Consider your dad is impressed with your performance in sport and offers to give you Rs 1, 00,000. Nevertheless, he gives you two options as mentioned below:

Which option would you choose? Why?

Despite the equal face value instinctively you would choose option 1 since you know the bird in the hand is better than two in the bush. Certainly, your decision to collect Rs 1, 00,000 today is a matured decision due to the following reasons:

Default risk
Inflation risk
Re-investment opportunities

Default Risk

Default risk is one of the most important reasons for you to choose option 1. What if your manager goes defaults on his promise to pay you Rs 1, 00,000 a year later. You have no control over that unforeseen future event and hence you have instinctively chosen to collect Rs 1, 00,000 today. Well! That’s a bright decision!

Inflation Risk

Inflation risk refers to how the value of goods and services changes (increases mostly) which undermines the value of your money. The value of money depreciates over a period due to inflation effects. That means the value of your money declines over some time due to the inflationary effect.

For example, an orange costs Rs 20 today, it is possible that it would cost you the same arrange Rs 40 a year later. This will decrease the purchasing power of your money over that period since the price has almost doubled in a matter of one year.

What is inflation? How does inflation connect with the time value of money

Generally, Inflation is caused by spiking prices of goods and services. The prices of goods are and services are largely considered to be impacted due to the mismatch in demand and supply factors. Keeping rest everything constant, the demand for a product rises when the supply is not able to match the quantity demanded and vice versa.

When the demand is more than the supply, the prices are expected to shoot up. On the other hand, when the supply is more than the quantity demanded, the prices are expected to fall.

Therefore, there is no point in waiting for one year to receive the same amount (Rs 1, 00,000). Instead, you choose to receive the same amount today and invest somewhere else so that you can offset the impact of inflation.

For example, consider the current inflation rate is say 5%, you need to earn a minimum of 5% returns on your money to offset the impact of inflation.

Re-investment opportunities

It is a wise decision to choose option 1 when you have a series of reinvestment opportunities that offer more than the current inflation rate. Many investment options offer good returns. When the inflation rate is 5% and you have options to earn more than that you should invest your money. The 5% return you earn will protect the value of your money while any returns above 5% would be your profits, to be precise your rewards for taking additional risk.

Therefore,

“The money earned today will have more value than the money that would be earned tomorrow”

“The money saved today will have more value than the money that would be saved tomorrow” and,

“The money invested today will have more value than the money that would be invested tomorrow”.

Broad areas of discussion in time value of money

Having understood the foundation concepts in the time value of money, let us now understand how to calculate the time value of money under two broad areas.

The topic can be discussed further under two broad areas.

What is Discounting?

Conversion of the future value of money into the present value of money.

What is Compounding?

Conversion of the present value of money into the future value of money.

Discounting

Conversion of the future value of money into the present value. The present value of money can be calculated using the equation shown below:

Where,

FV indicates the future value of money to be received

r indicates the reference rate or discount rate for the year

n indicates the period or number of years

Also Read: Scope of MBA Finance in 2022: Top Job Roles, Skills & Opportunities

Hypothetical case on discounting

Let us assume that, your reporting manager is impressed with the performance of the team during the last quarter. To encourage the team, the management has decided to offer an “employment continuance incentive”. Let us say the management offers an incentive with three alternatives.

Alternative 1: Receive Rs.1, 00,000 at the end of three years;

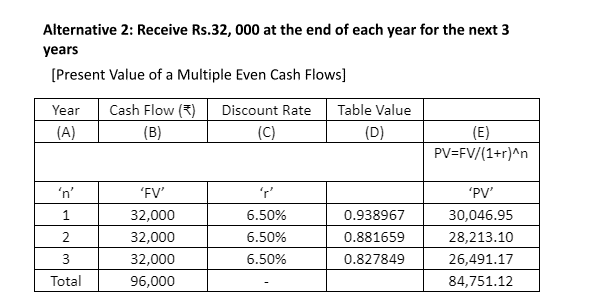
Alternative 2: Receive Rs.32, 000 at the end of each year for the next three years;

Alternative 3: Receive Rs.36, 000 at the end of the 1st year, Rs. 32,000 at the end of the second year, and Rs 28,000 at the end of the third year.

The management gives the team a day to decide on the alternative they want to opt for.

If you are part of this team, then which option would you choose and why?

Alternative 1: Receive Rs.1, 00,000 at the end of three years

Therefore, ₹84,751.12 today is equivalent to having ₹1, 00,000 after 3 years.

Note: Alternatively, you can use the following present value table to use the values

Period	0.01	0.02	0.03	0.04	0.05	0.06	0.07	0.08	0.09	0.1
1	0.990	0.980	0.971	0.962	0.952	0.943	0.935	0.926	0.917	0.909
2	0.980	0.961	0.943	0.925	0.907	0.890	0.873	0.857	0.842	0.826
3	0.971	0.942	0.915	0.889	0.864	0.840	0.816	0.794	0.772	0.751
4	0.961	0.924	0.888	0.855	0.823	0.792	0.763	0.735	0.708	0.683
5	0.951	0.906	0.863	0.822	0.784	0.747	0.713	0.681	0.650	0.621
6	0.942	0.888	0.837	0.790	0.746	0.705	0.666	0.630	0.596	0.564
7	0.933	0.871	0.813	0.760	0.711	0.665	0.623	0.583	0.547	0.513
8	0.923	0.853	0.789	0.731	0.677	0.627	0.582	0.540	0.502	0.467
9	0.914	0.837	0.766	0.703	0.645	0.592	0.544	0.500	0.460	0.424
10	0.905	0.820	0.744	0.676	0.614	0.558	0.508	0.463	0.422	0.386
11	0.896	0.804	0.722	0.650	0.585	0.527	0.475	0.429	0.388	0.350
12	0.887	0.788	0.701	0.625	0.557	0.497	0.444	0.397	0.356	0.319
13	0.879	0.773	0.681	0.601	0.530	0.469	0.415	0.368	0.326	0.290
14	0.870	0.758	0.661	0.577	0.505	0.442	0.388	0.340	0.299	0.263
15	0.861	0.743	0.642	0.555	0.481	0.417	0.362	0.315	0.275	0.239
16	0.853	0.728	0.623	0.534	0.458	0.394	0.339	0.292	0.252	0.218
17	0.844	0.714	0.605	0.513	0.436	0.371	0.317	0.270	0.231	0.198
18	0.836	0.700	0.587	0.494	0.416	0.350	0.296	0.250	0.212	0.180
19	0.828	0.686	0.570	0.475	0.396	0.331	0.277	0.232	0.194	0.164
20	0.820	0.673	0.554	0.456	0.377	0.312	0.258	0.215	0.178	0.149
25	0.780	0.610	0.478	0.375	0.295	0.233	0.184	0.146	0.116	0.092
30	0.742	0.552	0.412	0.308	0.231	0.174	0.131	0.099	0.075	0.057
35	0.706	0.500	0.355	0.253	0.181	0.130	0.094	0.068	0.049	0.036
40	0.672	0.453	0.307	0.208	0.142	0.097	0.067	0.046	0.032	0.022
50	0.608	0.372	0.228	0.141	0.087	0.054	0.034	0.021	0.013	0.009

Period	0.11	0.12	0.13	0.14	0.15	0.16	0.17	0.18	0.19	0.2
1	0.901	0.893	0.885	0.877	0.870	0.862	0.855	0.847	0.840	0.833
2	0.812	0.797	0.783	0.769	0.756	0.743	0.731	0.718	0.706	0.694
3	0.731	0.712	0.693	0.675	0.658	0.641	0.624	0.609	0.593	0.579
4	0.659	0.636	0.613	0.592	0.572	0.552	0.534	0.516	0.499	0.482
5	0.593	0.567	0.543	0.519	0.497	0.476	0.456	0.437	0.419	0.402
6	0.535	0.507	0.480	0.456	0.432	0.410	0.390	0.370	0.352	0.335
7	0.482	0.452	0.425	0.400	0.376	0.354	0.333	0.314	0.296	0.279
8	0.434	0.404	0.376	0.351	0.327	0.305	0.285	0.266	0.249	0.233
9	0.391	0.361	0.333	0.308	0.284	0.263	0.243	0.225	0.209	0.194
10	0.352	0.322	0.295	0.270	0.247	0.227	0.208	0.191	0.176	0.162
11	0.317	0.287	0.261	0.237	0.215	0.195	0.178	0.162	0.148	0.135
12	0.286	0.257	0.231	0.208	0.187	0.168	0.152	0.137	0.124	0.112
13	0.258	0.229	0.204	0.182	0.163	0.145	0.130	0.116	0.104	0.093
14	0.232	0.205	0.181	0.160	0.141	0.125	0.111	0.099	0.088	0.078
15	0.209	0.183	0.160	0.140	0.123	0.108	0.095	0.084	0.074	0.065
16	0.188	0.163	0.141	0.123	0.107	0.093	0.081	0.071	0.062	0.054
17	0.170	0.146	0.125	0.108	0.093	0.080	0.069	0.060	0.052	0.045
18	0.153	0.130	0.111	0.095	0.081	0.069	0.059	0.051	0.044	0.038
19	0.138	0.116	0.098	0.083	0.070	0.060	0.051	0.043	0.037	0.031
20	0.124	0.104	0.087	0.073	0.061	0.051	0.043	0.037	0.031	0.026
25	0.074	0.059	0.047	0.038	0.030	0.024	0.020	0.016	0.013	0.010
30	0.044	0.033	0.026	0.020	0.015	0.012	0.009	0.007	0.005	0.004
35	0.026	0.019	0.014	0.010	0.008	0.006	0.004	0.003	0.002	0.002
40	0.015	0.011	0.008	0.005	0.004	0.003	0.002	0.001	0.001	0.001
50	0.005	0.003	0.002	0.001	0.001	0.001	0.000	0.000	0.000	0.000

Alternative 3: Receive Rs.36, 000 at the end of the 1st year, Rs. 32,000 at the end of the second year, and Rs. 28,000 at the end of the third year

Year	Cash Flow (₹)	Discount Rate	Table Value	PV=FV/(1+r)^n
(A)	(B)	(C)	(D)	(E)
‘n’	‘FV’	‘r’		‘PV’
1	36,000	6.50%	0.938967	32,863.85
2	32,000	6.50%	0.881659	28,213.10
3	28,000	6.50%	0.827849	23,179.77
Total	96,000	–		84,256.72

Decision Time

Alternatives	Options to choose	Discounted Cash flows (₹)
1	Receive Rs.1,00,000 at the end of three years	82,784.91
2	Receive Rs.32,000 at the end of each year for the next 3 years	84,751.12
3	Receive Rs.36,000 at the end of the 1st year, Rs 32,000 at the end of the second year, and Rs 28,000 at the end of the third year	84,256.72

Among the three options available, alternative 2 is more attractive since it generates better positive cash flows compared to alternative 1 and alternative 3.

Alternative 2: ₹ 84,751.12

Compounding (Future value of money)

According to Einstein “Compound interest is the eighth wonder of the world.

He who understands it earns it … he who doesn’t … pays it.”

At first, this statement might seem like a bit of a hyperbole but the sums behind it display that it is not.

Compounding is also called the future value of money or the process of converting the present value of money into the future value of money. Compounding is considered to be one of the most powerful weapons in an arsenal of habitual investors. In simple language, compounding is a mathematical concept that helps the investor to make his/her money work for him. Compounding helps investment to grow due to the interest earned on principal as well as the accumulated interest added.

The compound is a process in which the earnings of investment are reinvested to generate further earnings over a while. This growth of earnings is calculated using the exponential functions that differ from the linear growth. In compounding, the present values of all the cash flows are converted into the future value of cash flow.

Four major factors determine the speed at which your money

Rate of return

At what rate of return you invest your money is something very determines the speed at which your money grows. Higher the return better the compounded value of your money over a period.

Time factor

Time plays a key role in determining the future value of your money. The value of money declines over a period which would result in the compounded value of your money also would decline.

Interest rates

Prevailing inflation rates will have bearing on the interest rates. Generally, the interest you earn on your investment would be a risk-free rate plus additional returns. The risk-free rates are calculated by the central bank of each country based on various parameters. Higher the interest rates bigger the returns on your investments.

Tax rates

Please note the income you earn is tax-deductible except for the situation where the individual is in the tax-free bracket.

Future Value Formula

FV_n = PV (1+r)ⁿ

Compounding Table

FV_n = PV * FVIF_r,n

Examples

What is the future value of ₹1,000 deposited for 3 years with a financial institution offering an 8% return per year?

Solution:

Given: PV = ₹1000; r = 8% = 0.08; n = 3 years

Solution

Given: PV = ₹1000; r = 8% = 0.08; n = 3 years

Alternatively,

You can refer to the FVIF table, where you can look for n = 3 and move horizontally, till we reach 8% where you will get the factor value as shown below:

Future value of the annuity

Future value interest factor of Re 1 per period at i% for n periods, FVIF(i,n)
Period	1%	2%	3%	4%	5%	6%	7%	8%	9%	10%
1	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
2	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
3	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
4	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
5	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
6	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
7	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
8	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
9	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
10	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
11	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
12	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
13	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
14	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
15	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
16	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
17	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
18	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
19	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
20	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000

On substituting this value in the equation we get:

FV=PV×FVIFr,n

FV=1000×FVIF8%,3=1000×1.26=₹1,260

Opportunity cost

Opportunity cost is a major pillar for the idea of the time value of money. Remember, money would grow only if is invested for a period and earn positive returns. The money that is kept in the safety lockers of your home would eventually lose over time.

Let’s take an example to have clarity on this concept. Consider you have invested Rs 10,000 in a stock anticipating an 11% return on the investment. You also had an opportunity to invest money in a fixed deposit at the promised rate of 9%. However, you have gone for option 1(invest Rs 10,000 in stock).

At the end of the year, due to unforeseen events like market fluctuations, the value of your investment has grown to Rs 10,500 an appreciation of just 5%. Now, had you invested your Rs 10,000 in fixed deposit, you would have safely earned Rs 900 on investment. So the difference of Rs 400 is an opportunity cost for you.

Let us consider that you are a popular financial consultant in Mumbai. A customer comes to you for financial advice. You are thinking about recommending your client to invest in gold that costs ₹85,000. You are certain that next year the gold will be worth ₹91,000 and assure ₹6,000 gain. Given that the guaranteed interest rate in a bank is 10%, should the client undertake investment in gold?

It is important to note that the more you invest at an early age, the more your money works for you in the long run and this helps you achieve financial freedom. It is a wise decision to start investing early to leverage the power of compounding.

Rule 72

Have you ever wondered how much time your money takes to become double? No surprise, it is one of the common questions we most of us often think through. Well! before we see the answer to these questions, let us try to understand a few essentials that run in the background to derive an answer to this question.

We all love to have money and we love our money growing more and more. Obtaining a rough estimate of how much our money or how much time it would take to become double is certainly not greed. It is a common tendency of a human being.

Understanding how to invest, where to invest, how much money to invest, and when to invest are critical questions in investment management. Of course, these questions are intimidating too. We may think of applying some formula that finds out how long your money takes to double? That is exactly something that Rule 72 does.

Rule 72 is a simplified version of logarithmic calculations using natural log numbers. The rule applies to anything that is expected to grow exponentially over a period. You can use Rule 72 To understand how much time it would take to grow or to become double.

Variations to the rule

There are a couple of more variations being used in investment analysis. For example, Rule 69 and 70. However, Rule 72 considered to be the most useful among the variations available.

Let us understand Rule 72 with a plain example

Suppose you want to invest Rs 1, 00,000 today at the compounded annual interest rate is 8%. How long will it take for your money to become double?

Years to double = 9 Years

Therefore, your money (Rs. 1, 00,000) will be doubled in 9 years

Annuity

What is annuity?

There are a series of options for those who are looking for planning their retirement. Annuities are the best methods out of all the available options. Annuities provide regular-stream cash inflows when you are faced with retirement or any other situation that blocks your income sources. Annuities can be customized to the requirement of each individual based on their needs.

Types of annuities

There are different categories of annuities. These categories are broadly classified based on different parameters as shown below:

Based on the underlying investment – Fixed or variable annuities
Basic purpose – Deferred or Immediate
Total value – Lump-sum annuity
Premium payment arrangement – Single premium or Flexible premium

Let us try to through light on some of the most popular annuities

Fixed annuities

As the name indicates, fixed annuities guarantee the principal and minimum rate of interest. Fixed annuities grows will not drop in value. In this case, the contributions need to be consistent throughout the period. Fixed annuities are the best investment methods for those who want to plan their retirement and reduce the risk. In fixed annuities, the cash flows for individuals are guaranteed for life and that is the reason fixed annuities are often called single-life annuities. Fixed annuities are easy to understand, simple to calculate and less complex than variable annuities. However, one of the limitations of a fixed annuity is that it does not offer protection against inflation.

Variable annuities

Variable annuities offer potentially higher returns than other categories of annuities. However, as we know the risk and return mostly go hand in hand, there is a level of risk involved in realizing these higher returns. In variable annuities, the money is invested in funds. These funds will have a definite set of objectives.

For example, a mutual fund that has an objective of generating higher returns may invest in stocks often in volatile stocks that generate a higher return(higher risk too). Nevertheless, the investors are asked to choose their preferences of returns based on which the funds invest on various investment options to meet the risk and return expectations.

Indexed Annuity

Indexed annuities are also termed fixed-indexed insurance products or equity-indexed annuities. These indexes may have the characteristics of fixed or variable annuities. The methods of calculating these annuities often become complex since the outcomes are market-driven.

Indexed annuities are generally fixed annuities in nature with a variable rate of interest that is linked to underlying market indexes like Sensex, CNX Nifty, S&P 500. These annuities offer assured minimum income benefits and potential upside returns are linked to the market.

One of the limitations of indexed equity is that upside potential is linked to participation rate or spread resulting in buyers of these annuities never keeping pace with a robust market.

Immediate annuities

In an immediate annuity, the premium is paid in a lump sum and certainly not on multiple occasions. Generally, those who are on the verge of retirement but wants to avail income every month with immediate effect buy immediate annuities.

Deferred Annuities

With the advent of technologies, advanced medical systems and increased awareness of health and fitness, life expectancy across the world is growing across the world. Due to this reason, many individuals plan their income post retirements. A deferred annuity is one such product to meet the objective in this case.

Deferred annuities are developed for long term savings. This is an insurance agreement that does not guarantee payouts immediately. Deferred annuity enables an individual to build a corpus which is later used to purchase an annuity. Deferred annuities are more attractive for those who want to guarantee in the future and do not have income on an immediate basis. However, they want to build the corpus and enable that corpus to work for him/her at retirement or any other unforeseen situation of income loss.

Lump-sum annuities

Most lump sum annuities in India offer regular cash payouts after a definite period. However, annuities are also paid in a lump sum after a specified period. It is important to note that complete retirement benefits would not be available to the individual as a lump-sum annuity amount.

Single premium annuity

Single premium annuities require only one-time payment at the time of initiation of the plan.

The possible benefit of a single premium deferred annuity is that the money may grow during the accumulation phase, depending on the type of annuity you purchase. With this type of annuity, you could allow it to grow until you need to start receiving payments. However, you also could lose access to your premium until the annuity matures. You’ll owe surrender charges if the contract is terminated within the surrender charge period. In contrast, a single premium immediate annuity may allow you to receive payments earlier without having to pay penalties or additional fees.

Flexible premium annuity

This plan allows investors to choose the amount and frequency of their choice for making the payment of annuities.

Perpetuity

What is perpetuity?

Perpetuity is one of the most important concepts in financial management. The concept of perpetuity helps value stocks of a company, value real estate cash flows, and many other investment opportunities. Perpetuity is one of the widely used methods to properly evaluate the returns of bonds, stocks, and real estate.

Perpetuity refers to a financial instrument that pays cashflows for an indefinite period. Perpetuities are used to recognize the present value of a company’s future projected cash flows and terminal value.

Perpetuity refers to a constant stream of cash flows with no end. The holder of this financial instrument is entitled to receive interest payments forever. These infinite series of cash flows can have a finite present value.

Nevertheless, cash payments are infinite, it is thinkable to compute their present total value since the value of each payment decreases with each year to the point that it approximates zero.

Perpetuity Formula

The formula used to calculate perpetuity is Cash flows divided by discount rate.

Present Value of Perpetuity =	A
r

Where,

A = amount/cash flow

r = interest rate

We can calculate perpetuity values using the perpetuity formula. It classically divides cash flow by a discount rate, which is the interest rate banks pay to borrow money from the Reserve Bank of India. So, if you were to receive Rs 10,000 every year incessantly, and the discount rate was 5%, the present value of your perpetuity would be 10,000 / 0.05 = Rs 200,000.

Let us understand the concept of perpetuity with another example shown below:

Calculate the present value on 31^st Dec 2021 of a perpetuity paying Rs 10,000 at the end of each month starting from 1^st Dec 2021. The monthly discount rate is 7%.

Present Value of Perpetuity =	A
r

Given that,

Periodic payment (A) = Rs 10,000

Discount rate = 0.07

Present Value (perpetuity) = Rs 10,000/0.07

= Rs 1, 42,857

Growing Perpetuity

Also called graduating perpetuity. A cash flow that is not only expected to be received for an indefinite period, but also grow with the same rate of growth forever.

Example,

What is the value of a promise to receive ₹ 10,000 next year, growing by 2% forever, if the interest rate is 8% per year?

Growing Perpetuity =	A
r-g

₹ 10,000/0.08-0.02 = ₹ 1, 66,667

Key Takeaways

Here is a quick recap of what we have learned in this article:

The value of money depreciates over some time due to the inflation effect.
Compounding refers to the conversion of the present value of money to the future value of money
Discounting refers to the conversion of the future value of money to the present value of money.
The rupee earned today will have more value than the money that would be earned tomorrow.
The rupee saved today will have more value than the money that would be saved tomorrow.
The rupee invested today will have more value than the money that would be invested tomorrow.
Perpetuity refers to a constant stream of cash flows with no end.
Growing perpetuity refers to a cash flow that is not only expected to be received for an indefinite period, but also grow with the same rate of growth forever.

That’s all in this article. I hope you enjoyed reading the article. Thank you!

Introduction to Corporate Finance | Corporate Finance Tutorial | Great Learning