Browse by Domains
Table of Contents

Insertion Sort in C, C++, Java and Python | Insertion sort algorithm

By Updated on Dec 13, 2022 15187
Table of contents

Insertion sort in c is the simple sorting algorithm that virtually splits the given array into sorted and unsorted parts, then the values from the unsorted parts are picked and placed at the correct position in the sorted part.

What is sorting? 

In simple words, sorting means logically arranging data, that is, either in ascending or descending order.

But, where can we see sorting in real life? Although you come across sorting many times in your life, you may not have noticed it. For instance, let us consider an example of a student, David, in class 7.  

He is assigned a task to arrange the mathematics test answer sheets in ascending order so that the student who scored the highest marks can be awarded. Let us assume that David completed the task and sorted the sheets in ascending order, and found that he was the one who scored the maximum marks. How can you justify this? This is because his sheet was at last in the stack(the bundle of the sheets), and since all the sheets were arranged in ascending order, so he was the one with the highest marks.

So he completed his task, but how did he do so? He used one of the many sorting techniques, for instance, say insertion sort.

Now that we are clear with the real-world examples of sorting, let us understand what is the use of sorting in computer science? There are plenty of uses.

For example:

  1. The contact list in your phone is sorted, which means you can easily access your desired contact from your phone since the data is arranged in that manner for you. In other words, “it is sorted”.
  2. While shopping on flip kart or amazon, you sort items based on your choice, that is, price low to high or high to low.
  3. The app docker on your phone is an easily relate-able example.

Now since we have a crystal clear idea about sorting in both perspectives, let us, deep-dive, into Insertion Sort in c.

Insertion Sort in c

Insertion sort in c is the simple sorting algorithm that virtually splits the given array into sorted and unsorted parts.

I hope you remember the task assigned to David. Let us assume David used the insertion sort technique to complete his task. Then he first chooses a number 1 as a pivot or origin, then starts with the other sheet and places the sheet with the marks and compares it with the marks on selected sheet number 1. If the sheet has fewer marks, he inserts it over and repeats the same process until he gets the sorted array.
Now speaking technically, the insertion sort follows the following algorithm to sort an array of size in ascending order:

1. Iterate from arr[1] to arr[n] over the array.
2. Compare the current element (key) to its predecessor.
3. If the key element is smaller than its predecessor, compare its elements before. Move the greater elements one position up to make space for the swapped element.

Example

Now let us apply the above algorithm for the task assigned to David and let the unsorted array of sheets be as follows:

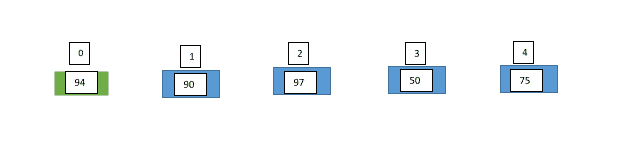
He first compared the sheet on index 0 (number 1) with the marks on the sheet. As index 1 is lesser than marks on the sheet at index 0, he inserts it on the left side of index 0. Now the new transformed array will look like this:

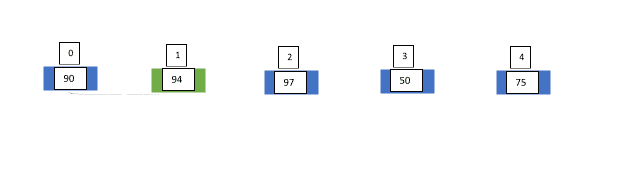
Note: The two elements at index 0 and index 1 have been swapped.

Now, he again compared the same selected sheet (number 1), which is now at index 1, with the marks on the sheet at index 2 and finds that it is greater than the selected sheet (number 1) that is it is already sorted. Our array would be:

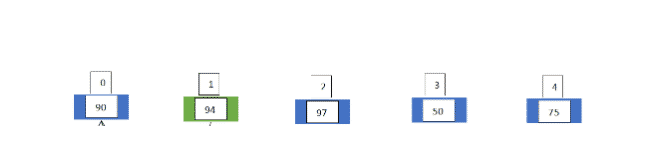
Now he again compares them. But this time, he compares the element at index 2 with the element at index 3, since the left part of index 2 is already sorted. He finds that the marks on index 3 are less than marks in the sheet at index 2, so he searches the right position for the sheet in the left (that is the sorted part) and finds the correct position at index 0. Now, the transformed array will be:

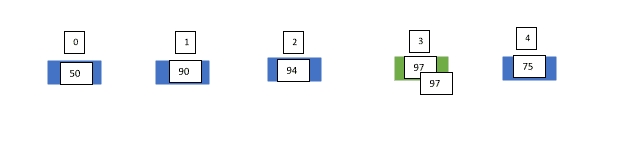
He again compares the element at index 3 with the element at index 4, and finds that marks on sheet at index 4 are less than on sheet at index 3. Thus, he finds the correct position for this element in the left (that is sorted part) and positioned it at index 1. Our sorted array will be:

So this is our sorted array. Now, can you tell how much David scored in his mathematics test? He scored 97 marks.

What is Insertion Sort Algorithm?

  • It is one of the easiest and brute force sorting algorithm
  • Insertion sort is used to sort elements in either ascending or descending order
  • In insertion sort, we maintain a sorted part and unsorted part
  • It works just like playing cards i.e, picking one card and sorting it with the cards that we have in our hand already 
  • With every iteration, one item is moved from the unsorted section to the sorted section
  • The first element is picked and is considered sorted
  • After this, we start picking from the second element onward and compare with elements in the sorted section
  • We keep shifting the elements from the sorted section one by one until an appropriate location is found for that element
  • This process is continued until all elements have been exhausted 

Insertion Sort Algorithm Pseudo-code

  • Take the first element and consider it to be a sorted part(a single element is always sorted)
  • Now pick arr[1] and store it is a temporary variable
  • Start comparing the values of tmp with elements of the sorted part from the rear side
  • If tmp is less than the rear element, say arr[k], then shift arr[k] to k+1 index
  • This shifting will continue until the appropriate location is identified. Then, we will put the temporary element at the identified location
  • This will continue for all the elements, and we will have our desired sorted array in ascending order

Also Read: Bubble Sort Algorithm

Insertion Sort Algorithm

Insertion sort in c

Insertion Sort(arr, size)
		consider 0th element as sorted part
  			for each element from i=2 to n-1
				tmp = arr[i]
				for j=i-1 to 0
					If a[j]>tmp
					  Then right shift it by one position
				put tmp at current j

Insertion Sort Dry Run

Input:

01234
2310161120

First step- marking of the sorted part

01234
2310161120

After i=1

01234
1023161120

After i=2

01234
1016231120

After i=3

01234
1011162320

After i=4

01234
1011162023

Insertion Sort Time Complexity

  • In the worst-case scenario, n will pick all elements and then n shifts to set it to the right position
  • In the best-case scenario, that is a sorted array, we will just pick the elements, but no shifting will take place leading it to n time complexity, that is, every element is traversed at least once
  • Best Time Complexity: O(n)
  • Average Time Complexity: O(n^2)
  • Worst Time Complexity: O(n^2)

Insertion Sort Space Complexity

  • No auxiliary space is required in insertion sort implementation. That is, we are not using any arrays, linked list, stack, queue, etc, to store our elements
  • Hence space complexity is: O(1)

Also Read: Facial Recognition using Python

Insertion Sort in C – Algorithm

Now let’s apply this algorithm on our insertion sort in C:

#include <stdio.h>
    // function to print the elements of the array
void display(int arr[], int n) {     
  for (int i = 0; i < n; i++) {
    printf("%d ", arr[i]);
  }
  printf("\n");
}
// function to sort the elements of the array
void insertionSort(int arr[], int n) {
  for (int i = 1; i < n; i++) {
    int tmp = arr[i];
    int j = i - 1;

    
    while (tmp < arr[j] && j >= 0) {
      arr[j + 1] = arr[j];
      --j;
    }
    arr[j + 1] = tmp;
  }
}
// main function or driver function
 int main() {
  int arr[] = {9, 5, 1, 4, 3};
  int n = sizeof(arr) / sizeof(arr[0]);
  printf("Elements before sorting:\n");
  display(arr, n);
  insertionSort(arr, n);
  printf("Elements after sorting:\n");
  display(arr, n);
}




Output of the program:
 Elements before sorting:
 9 5 1 4 3
 Elements after sorting:
 1 3 4 5 9

Insertion Sort in Java

import java.util.*;

class InsertionSort {

//method for sorting the elements
  void insertionSort(int arr[]) {
    int size = arr.length;

    for (int i = 1; i < size; i++) {
      int tmp = arr[i];
      int j = i - 1;

      
      while (j >= 0 && tmp < arr[j]) {
        arr[j + 1] = arr[j];
        --j;
      }

      arr[j + 1] = tmp;
    }
  }
	
  // method for printing the elements 
  void display(int arr[]) {
     int size = arr.length;
	 for (int i = 0; i < size; i++)
		System.out.print(arr[i]+" ");
	System.out.println();
	
   }
// Main method or driver method
  public static void main(String args[]) {
    int[] arr = { 9, 5, 1, 4, 3 };
    InsertionSort  ob = new InsertionSort();
    System.out.println("Elements before sorting: ");
    ob.display(arr);
    ob.insertionSort(arr);
    System.out.println("Elements after sorting: ");
    ob.display(arr);
  }
}


Output of the program:
Elements before sorting:
9 5 1 4 3
Elements after sorting:
1 3 4 5 9

Insertion Sort in C++ 

#include <iostream>
using namespace std;

//Function for displaying the elements
void display(int arr[], int size) {
  for (int i = 0; i < size; i++) {
    cout << arr[i] << " ";
  }
  cout << endl;
}

// Function for sorting the elements
void insertionSort(int arr[], int size) {
  for (int i = 1; i < size; i++) {
    int tmp = arr[i];
    int j = i - 1;  
    while (tmp < arr[j] && j >= 0) {
      arr[j + 1] = arr[j];
      --j;
    }
    arr[j + 1] = tmp;
  }
}

// Main Function or Driver Function 
int main() {
  int data[] = {9, 5, 1, 4, 3};
  int size = sizeof(data) / sizeof(data[0]);
  cout << “Elements before sorting:\n";
  display(data, size);
  insertionSort(data, size);
  cout << "Elements after sorting:\n";
  display(data, size);
}


Output of the program:
Elements before sorting:
9 5 1 4 3
Elements after sorting:
1 3 4 5 9 

// C++ program for insertion sort 
#include <bits/stdc++.h>
using namespace std;

/* Function to sort an array using insertion sort*/
void insertionSort(int arr[], int n) 
{ 
	int i, key, j; 
	for (i = 1; i < n; i++)
	{ 
		key = arr[i]; 
		j = i - 1; 

		/* Move elements of arr[0..i-1], that are 
		greater than key, to one position ahead 
		of their current position */
		while (j >= 0 && arr[j] > key)
		{ 
			arr[j + 1] = arr[j]; 
			j = j - 1; 
		} 
		arr[j + 1] = key; 
	} 
} 

// A utility function to print an array of size n 
void printArray(int arr[], int n) 
{ 
	int i; 
	for (i = 0; i < n; i++) 
		cout << arr[i] << " "; 
	cout << endl;
} 

/* Driver code */
int main() 
{ 
	int arr[] = { 94,90,97,50,75 }; 
	int n = sizeof(arr) / sizeof(arr[0]); 

	insertionSort(arr, n); 
	printArray(arr, n); 

	return 0; 
}

Output:

50 75 90 94 97

Insertion Sort in Python

// Code for sorting the elements
def insertionSort(arr):

    for i in range(1, len(arr)):
        tmp = arr[i]
        j = i - 1
        
                
        while j >= 0 and tmp < arr[j]:
            arr[j + 1] = arr[j]
            j = j - 1
        
        arr[j + 1] = tmp

// Main code or Driver Code
arr = [9, 5, 1, 4, 3]
print('Elements before sorting:')
print(arr)
insertionSort(arr)
print('Elements after sorting:')
print(arr)





Output of the program:
Elements before sorting:
[ 9, 5, 1, 4, 3]
Elements after sorting:
[1, 3, 4, 5, 9]

Also Read: Python Tutorial for beginners

Insertion Sort Example

Example1:

Given the linked list with unsorted data in it, we need to sort the data.

Example:

Input: -1->5->3->4->0

Output: -1->0->3->4->5

Code: JAVA

public class List {
 node head;
 node sorted;

//Structure of the node that is the data part and the next part which points the next node
 class node {
  int data;
  node next;

  public node(int data) {
   this.data = data;
  }
 }

 void insert(int data) {
  node newnode = new node(data);
  newnode.next = head;
  head = newnode;
 }

 void insertionSort(node headref) {
  sorted = null;
  node curr = headref;

  while (curr != null) {
   node next = curr.next;
   sortedInsert(curr);
   curr = next;
  }
  head = sorted;
 }


 void sortedInsert(node newnode) {
  if (sorted == null || sorted.data >= newnode.data) {
   newnode.next = sorted;
   sorted = newnode;
  } else {
   node curr = sorted;
   while (curr.next != null && curr.next.data < newnode.data) {
    curr = curr.next;
   }
   newnode.next = curr.next;
   curr.next = newnode;
  }
 }

 void print_list(node head) {
  while (head != null) {
   System.out.print(head.data + " ");
   head = head.next;
   }
   System.out.println();
 }

 public static void main(String[] args) {
  List list = new List();
  list.insert(5);
  list.insert(20);
  list.insert(4);
  list.insert(3);
  list.insert(30);
  System.out.println("Original list:");
  list.print_list(list.head);
  list.insertionSort(list.head);
  System.out.println("Sorted list:");
  list.print_list(list.head);
 }
}

Output of the program:

Original list:
5 20 4 3 30

Sorted list:
3 4 5 20 30

Insertion sort in C

#include<stdio.h> 
#include<stdlib.h> 

struct Node 
{ 
	int data; 
	struct Node* next; 
}; 

void sortedInsert(struct Node**, struct Node*); 

void insertionSort(struct Node **head_ref) 
{ 
	struct Node *sorted = NULL; 

	
	struct Node *curr = *head_ref; 
	while (curr != NULL) 
	{ 
		struct Node *next = curr->next; 

		sortedInsert(&sorted, curr); 

		curr = next; 
	} 

	*head_ref = sorted; 
} 


void sortedInsert(struct Node** head_ref, struct Node* new_node) 
{ 
	struct Node* curr; 
	if (*head_ref == NULL || (*head_ref)->data >= new_node->data) 
	{ 
		new_node->next = *head_ref; 
		*head_ref = new_node; 
	} 
	else
	{ 
		curr = *head_ref; 
		while (curr->next!=NULL && 
			curr->next->data < new_node->data) 
		{ 
			curr = curr->next; 
		} 
		new_node->next = curr->next; 
		curr->next = new_node; 
	} 
} 


void display(struct Node *head) 
{ 
	struct Node *tmp = head; 
	while(tmp != NULL) 
	{ 
		printf("%d ", tmp->data); 
		tmp = tmp->next; 
	} 
} 

void insert(struct Node** head_ref, int new_data) 
{ 
	struct Node* new_node = new Node; 

	new_node->data = new_data; 

	new_node->next = (*head_ref); 

	(*head_ref) = new_node; 
} 


int main() 
{ 
	struct Node *a = NULL; 
	insert(&a, 5); 
	insert(&a, 20); 
	insert(&a, 4); 
	insert(&a, 3); 
	insert(&a, 30); 

	printf("\nOriginal list:\n"); 
	display(a); 

	insertionSort(&a); 

	printf("\nSorted list:\n"); 
	display(a); 

	return 0; 
} 
Output of the program:

Original list:
5 20 4 3 30

Sorted list:
3 4 5 20 30

Example 2:

Given the array, which is a nearly sorted (or K sorted) array, we need to sort the elements in the array.

Example:

Input : {6, 5, 3, 2, 8, 10, 9}

            k = 3

Output : {2, 3, 5, 6, 8, 9, 10}

Code: JAVA

class Main{
    static void insertionSort(int A[], int size) 
    { 
        int i, k, j; 
        for (i = 1; i < size; i++) 
        { 
        	k = A[i]; 
        	j = i-1; 
        
        	
        	while (j >= 0 && A[j] > k) 
        	{ 
        		A[j+1] = A[j]; 
        		j = j-1; 
        	} 
        	A[j+1] = k; 
        } 
    } 
    
    public static void main (String[] args) {
        int a[]={2,7,5,9,3,1};
        insertionSort(a,6);
        
    }
}

Insertion sort in C

void insertionSort(int A[], int size) 
    { 
        int i, k, j; 
        for (i = 1; i < size; i++) 
        { 
        	k = A[i]; 
        	j = i-1; 
        
        	
        	while (j >= 0 && A[j] > k) 
        	{ 
        		A[j+1] = A[j]; 
        		j = j-1; 
        	} 
        	A[j+1] = k; 
        } 
    }

Get in-depth knowledge about programming languages

Programming Fundamentals Introduction to R Programming Problem Solving in Programming

Difference between Selection, Bubble and Insertion sort

1. In terms of algorithm

In Insertion sort, adjacent elements are compared and sorted if they are in wrong order. We select the smallest element and swap it with the 0th index element in the first iteration. This selection continues for n-1 elements and single element is already sorted. We will have array sorted by 1 element in every iteration.

Here, we create partitions of sorted and unsorted parts. One by one element from the sorted part is taken and sent to the unsorted part for checking and placing it to the right position in sorting using swaps.

2. In terms of time and space complexity

All 3 sort have O(n2) time complexity. But via flag variable, we can reduce the time complexity of Insertion and insertion to O(n) is best case. Space Complexity is the same for all i.e., O(1).


BestAverageWorstSpace
SelectionO(n2)O(n2)O(n2)O(1)
BubbleO(n)O(n2)O(n2)O(1)
InsertionO(n)O(n2)O(n2)O(1)

3. In terms of speed

Insertion sort may work best with an already sorted array and there is no need for any extra flag.

4. In terms of in-place

In-place states that the algorithm is in-place if it does not need extra memory barring some variable creation which counts to constant space. Selection and Insertion are in-place algorithms and do not require any auxiliary memory.

5. In terms of stability

Stability states that the algorithm is stable if the relative ordering of the same elements in the input and output array remains the same. Insertion and Insertion are stable algorithms but naive selection is not as swapping may cost stability.

SelectionBubbleInsertion
Select smallest in every iteration do single swapAdjacent swap of every element with the other element where ording is incorrectTake and put the element one by one and put it in the right place in the sorted part.
Best case time complexity is O(n2)Best case time complexity is O(n)Best case time complexity is O(n)
Works better than Insertion as no of swaps are significantly lowWorst efficiency as too many swaps are required in comparison to selection and insertionWorks better than Insertion as no of swaps are significantly low
It is in-placeIt is in-placeIt is in-place
Not stableStableStable

This brings us to the end of the blog on Insertion sort in c. We hope that you were able to learn more about the sorting algorithm. If you wish to learn more about such concepts and algorithms, check out Great Learning Academy’s Free Online Courses and upskill today!

Faizan Parvez
Faizan has been working as an Instructor of Data Structure and Algorithm for the last 1 year. He has expertise in languages such as Java, JavaScript, etc. He is a Subject Matter Expert in the field of Computer Science and a Competitive programmer. He has been working in technical content development and is a Research Analyst.
Recommended for you

Leave a Comment

Your email address will not be published. Required fields are marked *

Great Learning Free Online Courses
Scroll to Top