Heap Sort Algorithm: C, C++, Java and Python Implementation

Heap Sort is one of the best sorting methods being in-place and with no quadratic worst-case running time. It is a comparison based sorting technique based on a Binary Heap data structure. In this article, we are going to cover all these subtopics:

What is Heap
What is Heap Sort
What is Heapify
Heapsort Pseudo-code
Heapsort Algorithm
Heapsort Algorithm Dry Run
Heapsort Time complexity
Heapsort Space complexity
Applications of Heap Sort
Heapsort in C
Heapsort in JAVA
Heapsort in C++
Heapsort in Python
Heapsort Example
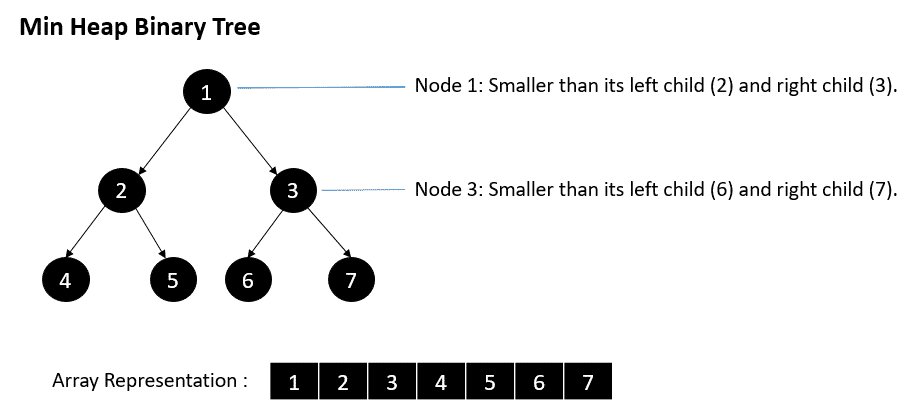
Difference between Min Heap & Max Heap
Which is better Mergesort or Heapsort

What is Heap

It is a data structure which is a complete binary tree
All the levels are completely filled except the last level
Heap has some order of values to be maintained between parents and their children
There are 2 variations of heap possible
- MIN HEAP
  - Here the value of parent is always less than the value of its children
  - Hence root will be the minimum in the entire heap
- MAX HEAP
  - Here the value of parent is always more than the value of its children
  - Hence root will be the maximum in the entire heap

What is Heap Sort

It is one of the efficient sorting algorithm based on heap data structure
Here the given array to be sorted is assumed to be a heap
So for ith index
- The left child will become the element present at the 2*i+1 index in the array
- The right child will become the element present at the 2*i+2 index in the array
- Parent of the ith index will be element present at (i-1)/2 index in the array

There are 2 major operations which are responsible for maintaining the heap
- Heapify
  - This operation sets the order of values between the parent and its child
  - If we are dealing with the max heap, it will find the index having max value among the node and its children
  - If the index holding max value is not the parent, it will wap the parent with the child having the max value
  - Algo

heapify(arr , i)
	leftChild = arr [2*0 + 1];
	rightChild = arr [2*0 + 2];
    	maxIndex = max( arr[i], leftChild, rightChild)
    	if(i != maxIndex)
          		swap(arr[i], arr[maxIndex])

Build MAXHEAP or MINHEAP
- This is responsible for setting parent-child order in the entire heap
- This is the first function which is called to build the heap
- It starts from the last parent in the tree because that is the first instance where the order may get disturbed
- So it iterates from i=n/2-1 to 0 and call heapify on every parent
- Algo

buildMaxHeap(arr)
	for(int i = n / 2 - 1; i >= 0; i--)
     		 heapify(arr, i);

In Heapsort, we deal with Maxheap.
As we know root will have the max value possible in the heap, we will swap it with the last element in the heap and reduce the heap size by 1.
Heap size is the variable that maintains the total number of elements to be considered in the heap
Then we call downward heapify on the root. It starts from setting the relationship between the root n d its children. If either of the children was maximum then heapify is called on it.

What is Heapify

The process of reshaping a binary tree into a Heap data structure is known as heapify. A binary tree is a tree data structure that has two child nodes at max. If a node’s children nodes are heapified, then only heapify process can be applied over that node. A heap should always be a complete binary tree, i.e., except the bottom level of the tree, all the levels are completely filled. The bottom level is filled from left to right. Bottom-up order should be used to perform heapification.

Example of Max-Heapify:

Let’s take an input array R=[11,22,25,5,14,17,2,18].
Step 1: To create a binary tree from the array:

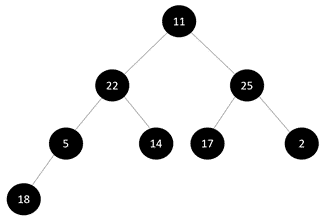
Step 2: Take a subtree at the lowest level and start checking if it follows the max-heap property or not:

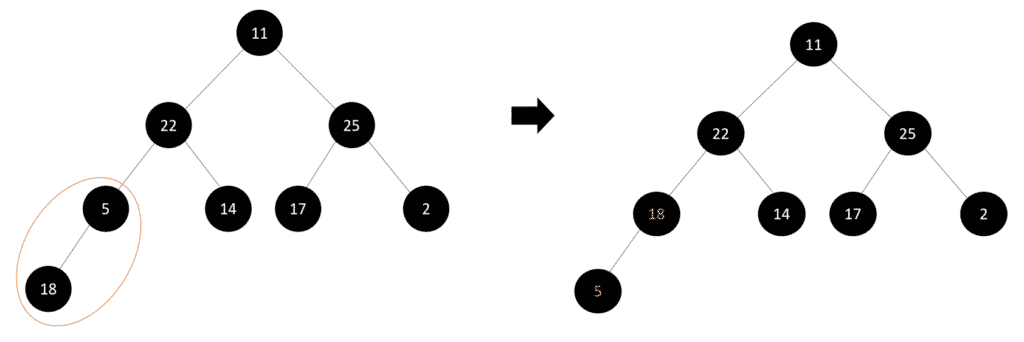
Step 3: Now, we can see that the subtree doesn’t follow the max-heap property. The children node must contain a lesser value than its parent node. We swap the key values between the parent node and the children node to ensure that the tree follows the max-heap property.
Let’s continue examining all the subtrees from the lowest level to the top level :

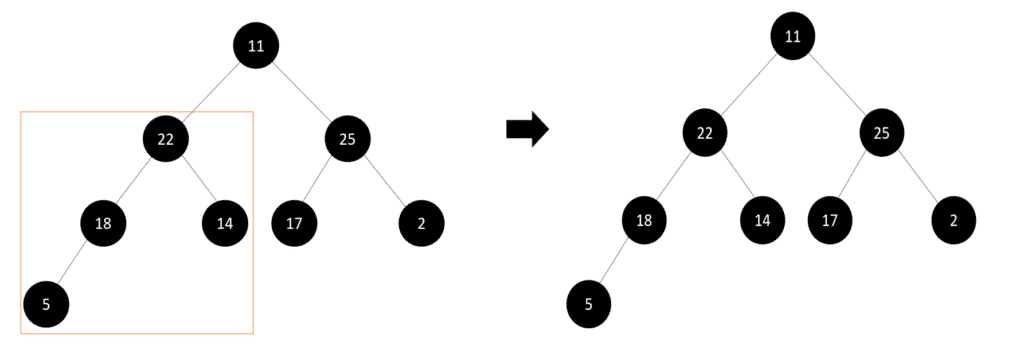
Step 4: We don’t need to change anything here as this subtree follows the max-heap property. Now, we look at the branches on the right side:

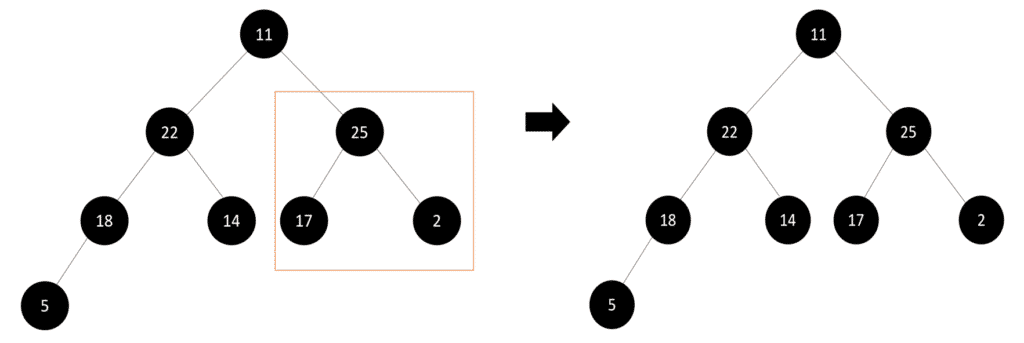
Step 5: Again the subtree follows the max-heap property so, let’s continue this process:

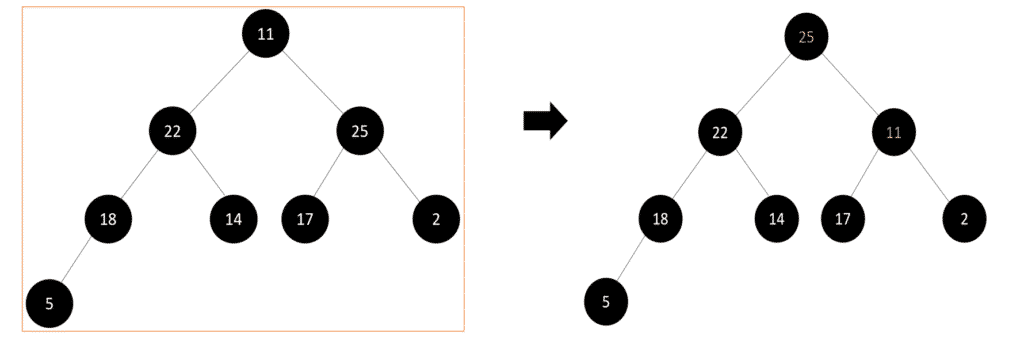
Step 6: Here again, we can see that the root node’s key value is not the largest among all the nodes in the tree. Hence, we swapped the root node’s key values with the key value of its right children node to match the max-heap property.
Now, after the swap, we need to check the right subtree from the root node to see whether it follows the max-heap property or not:

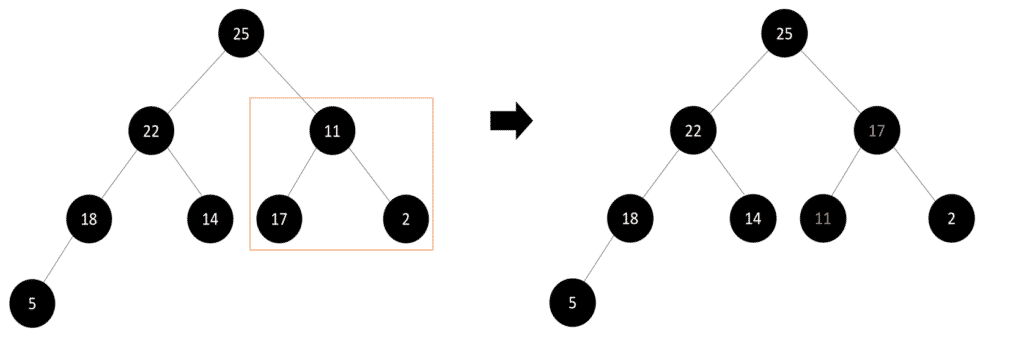
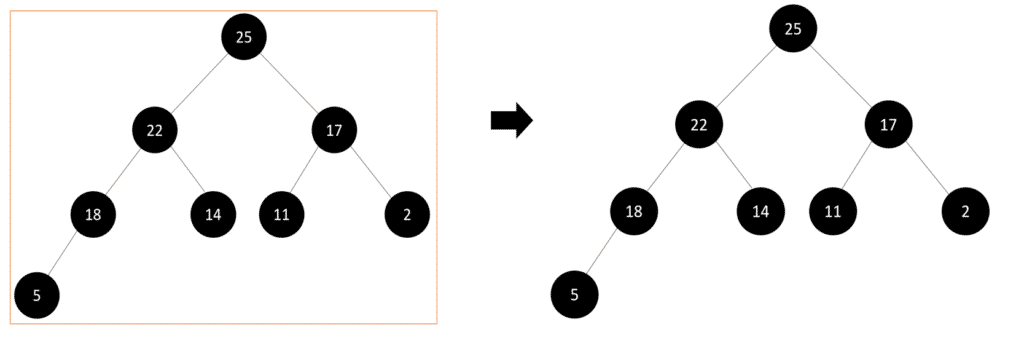
Step 7: Finally, we have to check the whole tree and see if it satisfies the max-heapify property, and then we’ll get our final max-heap tree:

Heapsort Pseudo-code

First, call build max heap to set the heap initially
Once the heap is created, take the root and wap it will the last element of the heap
Reduce the size of the heap
Call max heapify of index 0 i.e, the new root of the heap

Heapsort Algorithm

Heapsort(arr)
	buildMaxHeap(arr)
	for (int i = n - 1; i >= 0; i--) {
      	  swap(&arr[0], &arr[i]);
	  heapsize--;
	  maxHeapify(arr,0);
  	}

Heapsort Algorithm Dry Run

input:

0	1	2	3	4
23	10	16	11	20

The first step – call build max heap

0	1	2	3	4
23	20	16	11	10

For i=4

0	1	2	3	4
20	11	16	10	23

After i=3

0	1	2	3	4
16	11	10	20	23

After i=2

0	1	2	3	4
11	10	16	20	23

After i=1

0	1	2	3	4
10	11	16	20	23

After i=0

0	1	2	3	4
10	11	16	20	23

Heapsort Time Complexity

Build max heap takes O(n/2) time
We are calling for heapify inside the for loop, which may take the height of the heap in the worst case for all comparison. Therefore time complexity will become O(nlogn)
Best Time Complexity: O(nlogn)
Average Time Complexity: O(nlogn)
Worst Time Complexity: O(nlogn)

Heapsort Space Complexity

No auxiliary space is required in Heapsort implementation that is we are not using any arrays, linked list, stack, queue, etc to store our elements
Hence space complexity is: O(1)

Applications of Heap Sort

K sorted array
K largest or smallest elements in an array

As Quicksort and Merge sort are better in practice, the Heap sort algorithm has limited usage.

Heapsort in C

#include <stdio.h>
  
  void swap(int *a, int *b) {
    int tmp = *a;
    *a = *b;
    *b = tmp;
  }
  
  void heapify(int arr[], int n, int i) {
    int max = i; //Initialize max as root
    int leftChild = 2 * i + 1;
    int rightChild = 2 * i + 2;
  
    //If left child is greater than root
    if (leftChild < n && arr[leftChild] > arr[max])
      max = leftChild;
  
    //If right child is greater than max
    if (rightChild < n && arr[rightChild] > arr[max])
      max = rightChild;
  
    //If max is not root
    if (max != i) {
      swap(&arr[i], &arr[max]);
      //heapify the affected sub-tree recursively
      heapify(arr, n, max);
    }
  }

  //Main function to perform heap sort
  void heapSort(int arr[], int n) {
    //Rearrange array (building heap)
    for (int i = n / 2 - 1; i >= 0; i--)
      heapify(arr, n, i);
 
    //Extract elements from heap one by one
    for (int i = n - 1; i >= 0; i--) {
      swap(&arr[0], &arr[i]); //Current root moved to the end
  
      heapify(arr, i, 0); //calling max heapify on the heap reduced
    }
  }

  //print size of array n using utility function
  void display(int arr[], int n) {
    for (int i = 0; i < n; ++i)
      printf("%d ", arr[i]);
    printf("\n");
  }

  //Driver code
  int main() {
    int arr[] = {11, 34, 9, 5, 16, 10};
    int n = sizeof(arr) / sizeof(arr[0]);
	
    printf("Original array:\n");
    display(arr, n);
    heapSort(arr, n);
  
    printf("Sorted array:\n");
    display(arr, n);
  }

Output of the program:
 Original array:
 11 34 9 5 16 10 
 Sorted array:
 5 9 10 11 16 34

Heapsort in Java

  public class HeapSort {
  
    public void sort(int arr[]) {
      int n = arr.length;
  
      //Rearrange array (building heap)
      for (int i = n / 2 - 1; i >= 0; i--) {
        heapify(arr, n, i);
      }
  
      //Extract elements from heap one by one
      for (int i = n - 1; i >= 0; i--) {
        //Current root moved to the end
        int tmp = arr[0];
        arr[0] = arr[i];
        arr[i] = tmp;
  
        heapify(arr, i, 0);//calling max heapify on the heap reduced
      }
    }
  
    void heapify(int arr[], int n, int i) {
      int max = i; //Initialize max as root
      int leftChild = 2 * i + 1;
      int rightChild = 2 * i + 2;
  
      //If left child is greater than root
      if (leftChild < n && arr[leftChild] > arr[max])
        max = leftChild;
  
      //If right child is greater than max
      if (rightChild < n && arr[rightChild] > arr[max])
        max = rightChild;
  
      //If max is not root
      if (max != i) {
        int swap = arr[i];
        arr[i] = arr[max];
        arr[max] = swap;

        //heapify the affected sub-tree recursively
        heapify(arr, n, max);
      }
    }
  
    //print size of array n using utility function
    static void display(int arr[]) {
      int n = arr.length;
      for (int i = 0; i < n; ++i)
        System.out.print(arr[i] + " ");
      System.out.println();
    }
  
    //Driver code
    public static void main(String args[]) {
      int arr[] = {11, 34, 9, 5, 16, 10};
  
      HeapSort hs = new HeapSort();
      System.out.println("Original array:");
      display(arr);
	  hs.sort(arr);
  
      System.out.println("Sorted array:");
      display(arr);
    }
  }

Output of the program:
 Original array:
 11 34 9 5 16 10 
 Sorted array:
 5 9 10 11 16 34

Heapsort in C++

  
  #include <iostream>
  using namespace std;
  
  void heapify(int arr[], int n, int i) {
    int max = i; //Initialize max as root
    int leftChild = 2 * i + 1;
    int rightChild = 2 * i + 2;
  
    //If left child is greater than root
    if (leftChild < n && arr[leftChild] > arr[max])
      max = leftChild;
  
    //If right child is greater than max
    if (rightChild < n && arr[rightChild] > arr[max])
      max = rightChild;
  
    //If max is not root
    if (max != i) {
      swap(arr[i], arr[max]);
      heapify(arr, n, max); //heapify the affected sub-tree recursively
    }
  }
  
  //Main function to perform heap sort
  void heapSort(int arr[], int n) {
    //Rearrange array (building heap)
    for (int i = n / 2 - 1; i >= 0; i--)
      heapify(arr, n, i);
  
    //Extract elements from heap one by one
    for (int i = n - 1; i >= 0; i--) {
      swap(arr[0], arr[i]); //Current root moved to the end
  
      heapify(arr, i, 0); //calling max heapify on the heap reduced
    }
  }
  
  //print size of array n using utility function
  void display(int arr[], int n) {
    for (int i = 0; i < n; ++i)
      cout << arr[i] << " ";
    cout << "\n";
  }
  
  //Driver code
  int main() {
    int arr[] = {11, 34, 9, 5, 16, 10};
    int n = sizeof(arr) / sizeof(arr[0]);
    cout << "Original array:\n";
    display(arr, n);
    heapSort(arr, n);
  
    cout << "Sorted array:\n";
    display(arr, n);
  }

Output of the program:
 Original array:
 11 34 9 5 16 10 
 Sorted array:
 5 9 10 11 16 34

Heapsort in Python

def heapify(arr, n, i): 
    largest = i #Initialize max as root
    l = 2 * i + 1
    r = 2 * i + 2

    //If left child is greater than root
    if l < n and arr[i] < arr[l]:
      largest = l
    
    //If right child is greater than max
    if r < n and arr[largest] < arr[r]:
      largest = r

    //If max is not root
    if largest != i:
      arr[i], arr[largest] = arr[largest], arr[i]
      heapify(arr, n, largest) //heapify the root

//Main function to perform heap sort
def heapSort(arr):
  n = len(arr)

  #Build MaxHeap
  for i in range(n //2, -1, -1):
    heapify(arr, n, i)

  #Extract elements from heap one by one
  for i in range(n - 1, 0, -1): 
    arr[i], arr[0] = arr[0], arr[i]
    heapify(arr, i, 0)

#Driver code
arr = [11, 34, 9, 5, 16, 10] 
n = len(arr) 
print("Original array:") 
for i in range(n):       
    print("%d " % arr[i], end = '')
heapSort(arr) 
print("Sorted array:") 
for i in range(n):       
    print("%d " % arr[i], end = '')

Output of the program:
 Original array:
 11 34 9 5 16 10 
 Sorted array:
 5 9 10 11 16 34

Heapsort Example

Example:

Find the kth largest element in the array

Input : 11 34 9 5 16 10

k= 3

Output: 11

C Code

 #include <stdio.h>
  
  void swap(int *a, int *b) {
    int tmp = *a;
    *a = *b;
    *b = tmp;
  }
  
  void heapify(int arr[], int n, int i) {
    int max = i;
    int leftChild = 2 * i + 1;
    int rightChild = 2 * i + 2;
  
    if (leftChild < n && arr[leftChild] > arr[max])
      max = leftChild;
  
    if (rightChild < n && arr[rightChild] > arr[max])
      max = rightChild;
  
    if (max != i) {
      swap(&arr[i], &arr[max]);
      heapify(arr, n, max);
    }
  }
  
  void heapSort(int arr[], int n, int k) {
    for (int i = n / 2 - 1; i >= 0; i--)
      heapify(arr, n, i);
  
    for (int i = n - 1; i > k; i--) {
      swap(&arr[0], &arr[i]);
  
      heapify(arr, i, 0);
    }
    
    printf("%d ",arr[0]);
  }
  

  
  int main() {
    int arr[] = {11, 34, 9, 5, 16, 10};
    int n = sizeof(arr) / sizeof(arr[0]);

    heapSort(arr, n, 3);
  }

Java Code

 public class HeapSort {
  
    public void sort(int arr[], int k) {
      int n = arr.length;
  
      for (int i = n / 2 - 1; i >= 0; i--) {
        heapify(arr, n, i);
      }
  
      for (int i = n - 1; i > k; i--) {
        int tmp = arr[0];
        arr[0] = arr[i];
        arr[i] = tmp;
  
        heapify(arr, i, 0);
      }
      System.out.println(arr[0]);
    }
  
    void heapify(int arr[], int n, int i) {
      int max = i;
      int leftChild = 2 * i + 1;
      int rightChild = 2 * i + 2;
  
      if (leftChild < n && arr[leftChild] > arr[max])
        max = leftChild;
  
      if (rightChild < n && arr[rightChild] > arr[max])
        max = rightChild;
  
      if (max != i) {
        int swap = arr[i];
        arr[i] = arr[max];
        arr[max] = swap;
  
        heapify(arr, n, max);
      }
    }
  
    static void display(int arr[]) {
      int n = arr.length;
      for (int i = 0; i < n; ++i)
        System.out.print(arr[i] + " ");
      System.out.println();
    }
  
    public static void main(String args[]) {
      int arr[] = {11, 34, 9, 5, 16, 10};
  
      HeapSort hs = new HeapSort();

	  hs.sort(arr,3);

    }
  }

C++ Code

#include <iostream>
  using namespace std;
  
  void heapify(int arr[], int n, int i) {
    int max = i;
    int leftChild = 2 * i + 1;
    int rightChild = 2 * i + 2;
  
    if (leftChild < n && arr[leftChild] > arr[max])
      max = leftChild;
  
    if (rightChild < n && arr[rightChild] > arr[max])
      max = rightChild;
  
    if (max != i) {
      swap(arr[i], arr[max]);
      heapify(arr, n, max);
    }
  }
  
  void heapSort(int arr[], int n) {
    for (int i = n / 2 - 1; i >= 0; i--)
      heapify(arr, n, i);
  
    for (int i = n - 1; i >= 0; i--) {
      swap(arr[0], arr[i]);
  
      heapify(arr, i, 0);
    }
  }
  
  void display(int arr[], int n) {
    for (int i = 0; i < n; ++i)
      cout << arr[i] << " ";
    cout << "\n";
  }
  
  int main() {
    int arr[] = {11, 34, 9, 5, 16, 10};
    int n = sizeof(arr) / sizeof(arr[0]);
    cout << "Original array:\n";
    display(arr, n);
    heapSort(arr, n);
  
    cout << "Sorted array:\n";
    display(arr, n);
  }

Difference between Min Heap & Max Heap

Sno.	Min Heap	Max Heap
1.	The keys present at all of the children nodes should be greater than or equal to the key present at the root node.	The keys present at all the root nodes should be less than or equal to the key present at the root node.
2.	The key element present at the root node is the minimum key element.	The key element present at the root node is the maximum key element.
3.	Ascending priority is used in Min-Heap.	Descending priority is used in Max-Heap.
4.	The smallest element has the priority in the construction of a Min-Heap.	The largest element has the priority in the construction of a Max-Heap.
5.	The first element to be popped from the heap in a Min-Heap is the smallest element.	The first element to be popped from the heap in a Min-Heap is the smallest element.

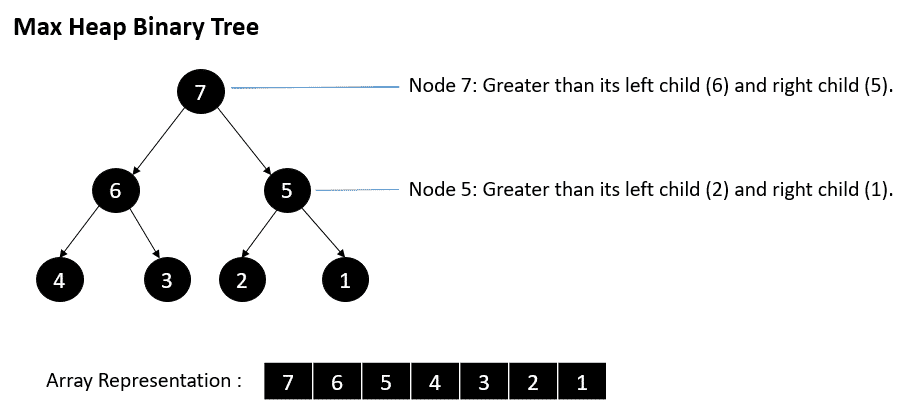
Which is better Mergesort or Heapsort

In terms of algorithm
- In merge sort, in every iteration, we divide the problem into 2 almost equal subproblems. Once no more dividing is possible, we start merging upwards
- In heap sort, there are 2 major operations that basically aids heapsort that is heapify and build heap

In terms of time and space complexity
- Merge sort take n extra space
- Heap sort make all the changes in the input array itself hence space requirement is constant here

	Best	Average	Worst	Space
Heap	O(nlogn)	O(nlogn)	O(nlogn)	O(1)
Merge	O(nlogn)	O(nlogn)	O(nlogn)	O(n)

In terms of speed
- Heapsort is a bit slower than merge sort

In terms of in-place
- In-place states that the algorithm is in-place if it does not need extra memory barring some variable creation which counts to constant space.
- Heap sort does not require any auxiliary memory but merge sort is out place.

In terms of stability
- Stability states that the algorithm is stable if the relative ordering of the same elements in the input and output array remains the same.
- Merge sort is stable algorithms but heap sort is not as swapping may cost stability.

This brings us to the end of this article where we learned about heap sort. To get a free course on data structures and algorithms, click on the banner below. Also, visit the great learning academy to see all the free courses we are providing.