- What is Heap
- What is Heap Sort
- What is Heapify
- Heapsort Pseudo-code
- Heapsort Algorithm
- Heapsort Algorithm Dry Run
- Heapsort Time Complexity
- Heapsort Space Complexity
- Applications of Heap Sort
- Heapsort in C
- Heapsort in Java
- Heapsort in C++
- Heapsort in Python
- Heapsort Example
- Difference between Min Heap & Max Heap
- Which is better Mergesort or Heapsort
Heap Sort is one of the best sorting methods being in-place and with no quadratic worst-case running time. It is a comparison based sorting technique based on a Binary Heap data structure. In this article, we are going to cover all these subtopics:
What is Heap
- It is a data structure which is a complete binary tree
- All the levels are completely filled except the last level
- Heap has some order of values to be maintained between parents and their children
- There are 2 variations of heap possible
- MIN HEAP
- Here the value of parent is always less than the value of its children
- Hence root will be the minimum in the entire heap
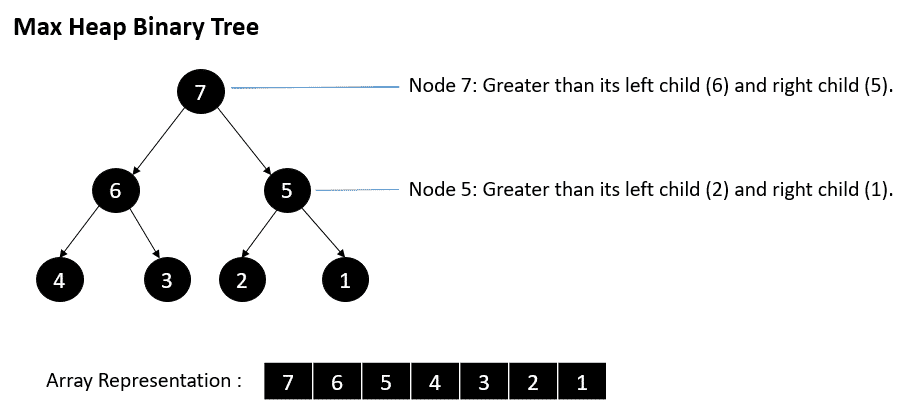
- MAX HEAP
- Here the value of parent is always more than the value of its children
- Hence root will be the maximum in the entire heap
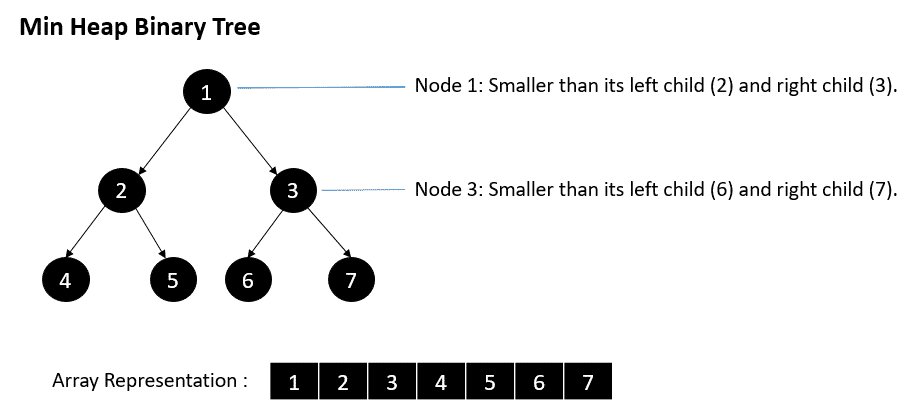
- MIN HEAP
What is Heap Sort
- It is one of the efficient sorting algorithm based on heap data structure
- Here the given array to be sorted is assumed to be a heap
- So for ith index
- The left child will become the element present at the 2*i+1 index in the array
- The right child will become the element present at the 2*i+2 index in the array
- Parent of the ith index will be element present at (i-1)/2 index in the array
- There are 2 major operations which are responsible for maintaining the heap
- Heapify
- This operation sets the order of values between the parent and its child
- If we are dealing with the max heap, it will find the index having max value among the node and its children
- If the index holding max value is not the parent, it will wap the parent with the child having the max value
- Algo
- Heapify
heapify(arr , i)
leftChild = arr [2*0 + 1];
rightChild = arr [2*0 + 2];
maxIndex = max( arr[i], leftChild, rightChild)
if(i != maxIndex)
swap(arr[i], arr[maxIndex])- Build MAXHEAP or MINHEAP
- This is responsible for setting parent-child order in the entire heap
- This is the first function which is called to build the heap
- It starts from the last parent in the tree because that is the first instance where the order may get disturbed
- So it iterates from i=n/2-1 to 0 and call heapify on every parent
- Algo
buildMaxHeap(arr)
for(int i = n / 2 - 1; i >= 0; i--)
heapify(arr, i);
- In Heapsort, we deal with Maxheap.
- As we know root will have the max value possible in the heap, we will swap it with the last element in the heap and reduce the heap size by 1.
- Heap size is the variable that maintains the total number of elements to be considered in the heap
- Then we call downward heapify on the root. It starts from setting the relationship between the root n d its children. If either of the children was maximum then heapify is called on it.
What is Heapify
The process of reshaping a binary tree into a Heap data structure is known as heapify. A binary tree is a tree data structure that has two child nodes at max. If a node’s children nodes are heapified, then only heapify process can be applied over that node. A heap should always be a complete binary tree, i.e., except the bottom level of the tree, all the levels are completely filled. The bottom level is filled from left to right. Bottom-up order should be used to perform heapification.
Example of Max-Heapify:
Let’s take an input array R=[11,22,25,5,14,17,2,18].
Step 1: To create a binary tree from the array:
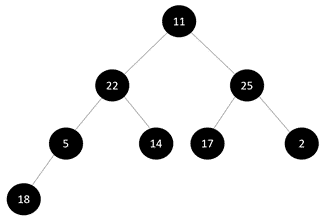
Step 2: Take a subtree at the lowest level and start checking if it follows the max-heap property or not:
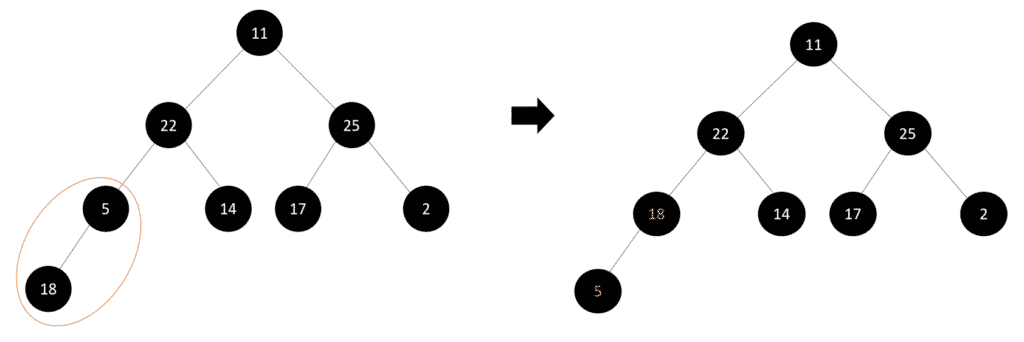
Step 3: Now, we can see that the subtree doesn’t follow the max-heap property. The children node must contain a lesser value than its parent node. We swap the key values between the parent node and the children node to ensure that the tree follows the max-heap property.
Let’s continue examining all the subtrees from the lowest level to the top level :
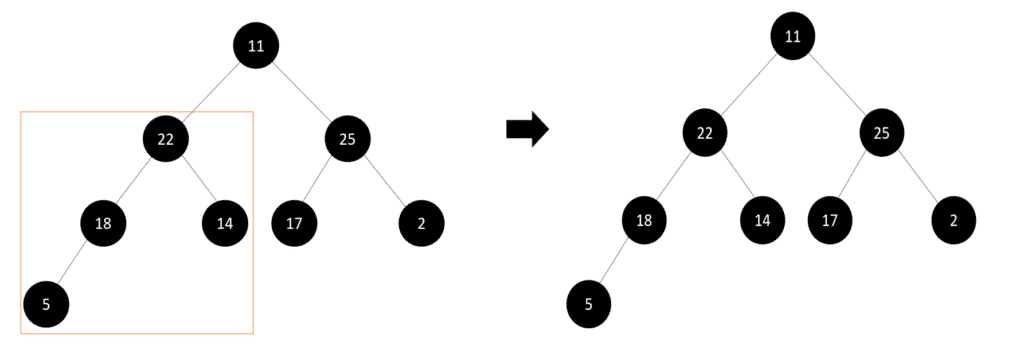
Step 4: We don’t need to change anything here as this subtree follows the max-heap property. Now, we look at the branches on the right side:
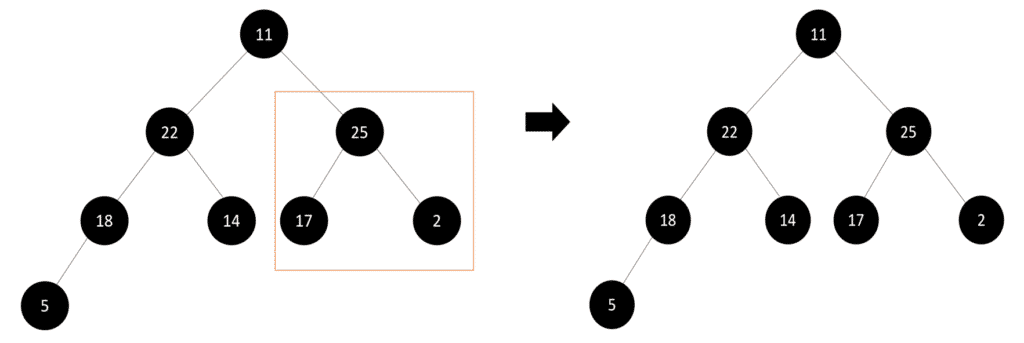
Step 5: Again the subtree follows the max-heap property so, let’s continue this process:
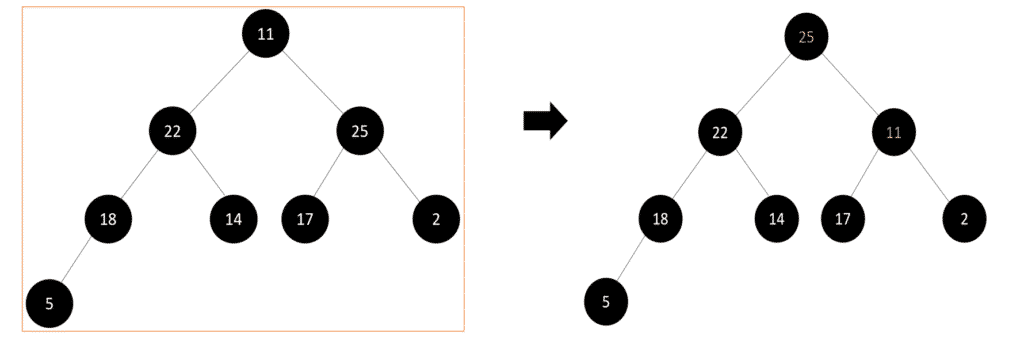
Step 6: Here again, we can see that the root node’s key value is not the largest among all the nodes in the tree. Hence, we swapped the root node’s key values with the key value of its right children node to match the max-heap property.
Now, after the swap, we need to check the right subtree from the root node to see whether it follows the max-heap property or not:
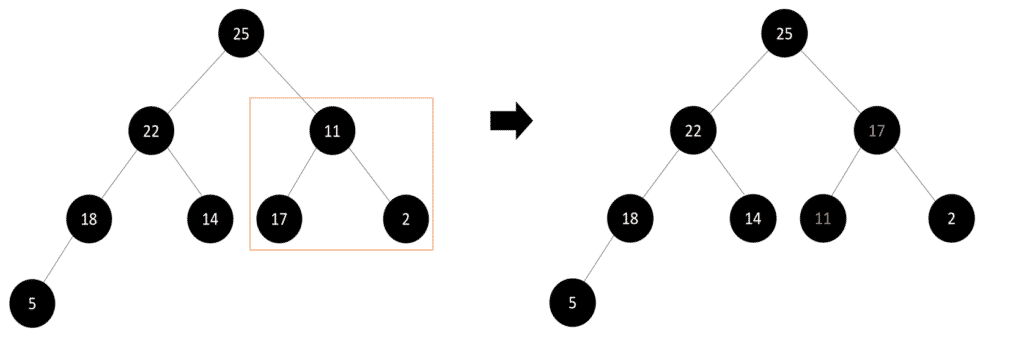
Step 7: Finally, we have to check the whole tree and see if it satisfies the max-heapify property, and then we’ll get our final max-heap tree:
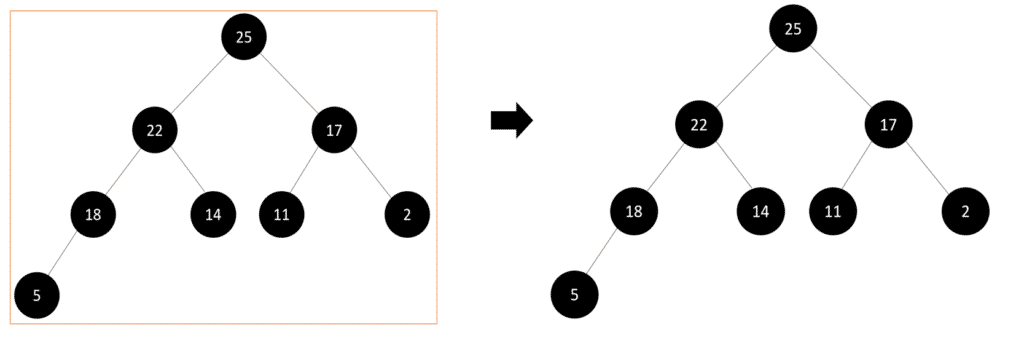
Heapsort Pseudo-code
- First, call build max heap to set the heap initially
- Once the heap is created, take the root and wap it will the last element of the heap
- Reduce the size of the heap
- Call max heapify of index 0 i.e, the new root of the heap
Heapsort Algorithm
Heapsort(arr)
buildMaxHeap(arr)
for (int i = n - 1; i >= 0; i--) {
swap(&arr[0], &arr[i]);
heapsize--;
maxHeapify(arr,0);
}
Heapsort Algorithm Dry Run
input:
| 0 | 1 | 2 | 3 | 4 |
| 23 | 10 | 16 | 11 | 20 |
The first step – call build max heap
| 0 | 1 | 2 | 3 | 4 |
| 23 | 20 | 16 | 11 | 10 |
For i=4
| 0 | 1 | 2 | 3 | 4 |
| 20 | 11 | 16 | 10 | 23 |
After i=3
| 0 | 1 | 2 | 3 | 4 |
| 16 | 11 | 10 | 20 | 23 |
After i=2
| 0 | 1 | 2 | 3 | 4 |
| 11 | 10 | 16 | 20 | 23 |
After i=1
| 0 | 1 | 2 | 3 | 4 |
| 10 | 11 | 16 | 20 | 23 |
After i=0
| 0 | 1 | 2 | 3 | 4 |
| 10 | 11 | 16 | 20 | 23 |
Heapsort Time Complexity
- Build max heap takes O(n/2) time
- We are calling for heapify inside the for loop, which may take the height of the heap in the worst case for all comparison. Therefore time complexity will become O(nlogn)
- Best Time Complexity: O(nlogn)
- Average Time Complexity: O(nlogn)
- Worst Time Complexity: O(nlogn)
Heapsort Space Complexity
- No auxiliary space is required in Heapsort implementation that is we are not using any arrays, linked list, stack, queue, etc to store our elements
- Hence space complexity is: O(1)
Applications of Heap Sort
- K sorted array
- K largest or smallest elements in an array
As Quicksort and Merge sort are better in practice, the Heap sort algorithm has limited usage.
Heapsort in C
#include <stdio.h>
void swap(int *a, int *b) {
int tmp = *a;
*a = *b;
*b = tmp;
}
void heapify(int arr[], int n, int i) {
int max = i; //Initialize max as root
int leftChild = 2 * i + 1;
int rightChild = 2 * i + 2;
//If left child is greater than root
if (leftChild < n && arr[leftChild] > arr[max])
max = leftChild;
//If right child is greater than max
if (rightChild < n && arr[rightChild] > arr[max])
max = rightChild;
//If max is not root
if (max != i) {
swap(&arr[i], &arr[max]);
//heapify the affected sub-tree recursively
heapify(arr, n, max);
}
}
//Main function to perform heap sort
void heapSort(int arr[], int n) {
//Rearrange array (building heap)
for (int i = n / 2 - 1; i >= 0; i--)
heapify(arr, n, i);
//Extract elements from heap one by one
for (int i = n - 1; i >= 0; i--) {
swap(&arr[0], &arr[i]); //Current root moved to the end
heapify(arr, i, 0); //calling max heapify on the heap reduced
}
}
//print size of array n using utility function
void display(int arr[], int n) {
for (int i = 0; i < n; ++i)
printf("%d ", arr[i]);
printf("n");
}
//Driver code
int main() {
int arr[] = {11, 34, 9, 5, 16, 10};
int n = sizeof(arr) / sizeof(arr[0]);
printf("Original array:n");
display(arr, n);
heapSort(arr, n);
printf("Sorted array:n");
display(arr, n);
}
Output of the program: Original array: 11 34 9 5 16 10 Sorted array: 5 9 10 11 16 34
Heapsort in Java
public class HeapSort {
public void sort(int arr[]) {
int n = arr.length;
//Rearrange array (building heap)
for (int i = n / 2 - 1; i >= 0; i--) {
heapify(arr, n, i);
}
//Extract elements from heap one by one
for (int i = n - 1; i >= 0; i--) {
//Current root moved to the end
int tmp = arr[0];
arr[0] = arr[i];
arr[i] = tmp;
heapify(arr, i, 0);//calling max heapify on the heap reduced
}
}
void heapify(int arr[], int n, int i) {
int max = i; //Initialize max as root
int leftChild = 2 * i + 1;
int rightChild = 2 * i + 2;
//If left child is greater than root
if (leftChild < n && arr[leftChild] > arr[max])
max = leftChild;
//If right child is greater than max
if (rightChild < n && arr[rightChild] > arr[max])
max = rightChild;
//If max is not root
if (max != i) {
int swap = arr[i];
arr[i] = arr[max];
arr[max] = swap;
//heapify the affected sub-tree recursively
heapify(arr, n, max);
}
}
//print size of array n using utility function
static void display(int arr[]) {
int n = arr.length;
for (int i = 0; i < n; ++i)
System.out.print(arr[i] + " ");
System.out.println();
}
//Driver code
public static void main(String args[]) {
int arr[] = {11, 34, 9, 5, 16, 10};
HeapSort hs = new HeapSort();
System.out.println("Original array:");
display(arr);
hs.sort(arr);
System.out.println("Sorted array:");
display(arr);
}
}
Output of the program: Original array: 11 34 9 5 16 10 Sorted array: 5 9 10 11 16 34
Heapsort in C++
#include <iostream>
using namespace std;
void heapify(int arr[], int n, int i) {
int max = i; //Initialize max as root
int leftChild = 2 * i + 1;
int rightChild = 2 * i + 2;
//If left child is greater than root
if (leftChild < n && arr[leftChild] > arr[max])
max = leftChild;
//If right child is greater than max
if (rightChild < n && arr[rightChild] > arr[max])
max = rightChild;
//If max is not root
if (max != i) {
swap(arr[i], arr[max]);
heapify(arr, n, max); //heapify the affected sub-tree recursively
}
}
//Main function to perform heap sort
void heapSort(int arr[], int n) {
//Rearrange array (building heap)
for (int i = n / 2 - 1; i >= 0; i--)
heapify(arr, n, i);
//Extract elements from heap one by one
for (int i = n - 1; i >= 0; i--) {
swap(arr[0], arr[i]); //Current root moved to the end
heapify(arr, i, 0); //calling max heapify on the heap reduced
}
}
//print size of array n using utility function
void display(int arr[], int n) {
for (int i = 0; i < n; ++i)
cout << arr[i] << " ";
cout << "n";
}
//Driver code
int main() {
int arr[] = {11, 34, 9, 5, 16, 10};
int n = sizeof(arr) / sizeof(arr[0]);
cout << "Original array:n";
display(arr, n);
heapSort(arr, n);
cout << "Sorted array:n";
display(arr, n);
}
Output of the program: Original array: 11 34 9 5 16 10 Sorted array: 5 9 10 11 16 34
Heapsort in Python
def heapify(arr, n, i):
largest = i #Initialize max as root
l = 2 * i + 1
r = 2 * i + 2
//If left child is greater than root
if l < n and arr[i] < arr[l]:
largest = l
//If right child is greater than max
if r < n and arr[largest] < arr[r]:
largest = r
//If max is not root
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i]
heapify(arr, n, largest) //heapify the root
//Main function to perform heap sort
def heapSort(arr):
n = len(arr)
#Build MaxHeap
for i in range(n //2, -1, -1):
heapify(arr, n, i)
#Extract elements from heap one by one
for i in range(n - 1, 0, -1):
arr[i], arr[0] = arr[0], arr[i]
heapify(arr, i, 0)
#Driver code
arr = [11, 34, 9, 5, 16, 10]
n = len(arr)
print("Original array:")
for i in range(n):
print("%d " % arr[i], end = '')
heapSort(arr)
print("Sorted array:")
for i in range(n):
print("%d " % arr[i], end = '')
Output of the program: Original array: 11 34 9 5 16 10 Sorted array: 5 9 10 11 16 34
Heapsort Example
Example:
Find the kth largest element in the array
Input : 11 34 9 5 16 10
k= 3
Output: 11
C Code
#include <stdio.h>
void swap(int *a, int *b) {
int tmp = *a;
*a = *b;
*b = tmp;
}
void heapify(int arr[], int n, int i) {
int max = i;
int leftChild = 2 * i + 1;
int rightChild = 2 * i + 2;
if (leftChild < n && arr[leftChild] > arr[max])
max = leftChild;
if (rightChild < n && arr[rightChild] > arr[max])
max = rightChild;
if (max != i) {
swap(&arr[i], &arr[max]);
heapify(arr, n, max);
}
}
void heapSort(int arr[], int n, int k) {
for (int i = n / 2 - 1; i >= 0; i--)
heapify(arr, n, i);
for (int i = n - 1; i > k; i--) {
swap(&arr[0], &arr[i]);
heapify(arr, i, 0);
}
printf("%d ",arr[0]);
}
int main() {
int arr[] = {11, 34, 9, 5, 16, 10};
int n = sizeof(arr) / sizeof(arr[0]);
heapSort(arr, n, 3);
}
Java Code
public class HeapSort {
public void sort(int arr[], int k) {
int n = arr.length;
for (int i = n / 2 - 1; i >= 0; i--) {
heapify(arr, n, i);
}
for (int i = n - 1; i > k; i--) {
int tmp = arr[0];
arr[0] = arr[i];
arr[i] = tmp;
heapify(arr, i, 0);
}
System.out.println(arr[0]);
}
void heapify(int arr[], int n, int i) {
int max = i;
int leftChild = 2 * i + 1;
int rightChild = 2 * i + 2;
if (leftChild < n && arr[leftChild] > arr[max])
max = leftChild;
if (rightChild < n && arr[rightChild] > arr[max])
max = rightChild;
if (max != i) {
int swap = arr[i];
arr[i] = arr[max];
arr[max] = swap;
heapify(arr, n, max);
}
}
static void display(int arr[]) {
int n = arr.length;
for (int i = 0; i < n; ++i)
System.out.print(arr[i] + " ");
System.out.println();
}
public static void main(String args[]) {
int arr[] = {11, 34, 9, 5, 16, 10};
HeapSort hs = new HeapSort();
hs.sort(arr,3);
}
}
C++ Code
#include <iostream>
using namespace std;
void heapify(int arr[], int n, int i) {
int max = i;
int leftChild = 2 * i + 1;
int rightChild = 2 * i + 2;
if (leftChild < n && arr[leftChild] > arr[max])
max = leftChild;
if (rightChild < n && arr[rightChild] > arr[max])
max = rightChild;
if (max != i) {
swap(arr[i], arr[max]);
heapify(arr, n, max);
}
}
void heapSort(int arr[], int n) {
for (int i = n / 2 - 1; i >= 0; i--)
heapify(arr, n, i);
for (int i = n - 1; i >= 0; i--) {
swap(arr[0], arr[i]);
heapify(arr, i, 0);
}
}
void display(int arr[], int n) {
for (int i = 0; i < n; ++i)
cout << arr[i] << " ";
cout << "n";
}
int main() {
int arr[] = {11, 34, 9, 5, 16, 10};
int n = sizeof(arr) / sizeof(arr[0]);
cout << "Original array:n";
display(arr, n);
heapSort(arr, n);
cout << "Sorted array:n";
display(arr, n);
}
Difference between Min Heap & Max Heap
| Sno. | Min Heap | Max Heap |
| 1. | The keys present at all of the children nodes should be greater than or equal to the key present at the root node. | The keys present at all the root nodes should be less than or equal to the key present at the root node. |
| 2. | The key element present at the root node is the minimum key element. | The key element present at the root node is the maximum key element. |
| 3. | Ascending priority is used in Min-Heap. | Descending priority is used in Max-Heap. |
| 4. | The smallest element has the priority in the construction of a Min-Heap. | The largest element has the priority in the construction of a Max-Heap. |
| 5. | The first element to be popped from the heap in a Min-Heap is the smallest element. | The first element to be popped from the heap in a Min-Heap is the smallest element. |
Which is better Mergesort or Heapsort
- In terms of algorithm
- In merge sort, in every iteration, we divide the problem into 2 almost equal subproblems. Once no more dividing is possible, we start merging upwards
- In heap sort, there are 2 major operations that basically aids heapsort that is heapify and build heap
- In terms of time and space complexity
- Merge sort take n extra space
- Heap sort make all the changes in the input array itself hence space requirement is constant here
| Best | Average | Worst | Space | |
| Heap | O(nlogn) | O(nlogn) | O(nlogn) | O(1) |
| Merge | O(nlogn) | O(nlogn) | O(nlogn) | O(n) |
- In terms of speed
- Heapsort is a bit slower than merge sort
- In terms of in-place
- In-place states that the algorithm is in-place if it does not need extra memory barring some variable creation which counts to constant space.
- Heap sort does not require any auxiliary memory but merge sort is out place.
- In terms of stability
- Stability states that the algorithm is stable if the relative ordering of the same elements in the input and output array remains the same.
- Merge sort is stable algorithms but heap sort is not as swapping may cost stability.
This brings us to the end of this article where we learned about heap sort. To get a free course on data structures and algorithms, click on the banner below. Also, visit the great learning academy to see all the free courses we are providing.







