Introduction to Multivariate Regression Analysis

Contributed by: Pooja Korwar

What is Multivariate Regression?

Multivariate regression shows the linear relationship between more than one predictor or independent variable and more than one output or dependent variable.

In comparison, simple regression refers to the linear relationship between one predictor and the output variable.

It is a supervised machine learning algorithm involving multiple data variables for analyzing and predicting the output based on various independent variables.

Multivariate regression tries to find a formula that can explain how variable factors respond simultaneously to changes in others. Follow along to learn more about it through some real-life examples.

Examples of Multivariate Regression

In today’s world, data is everywhere. Data is just facts and figures that provide meaningful information if analyzed properly.

Hence, data analysis is essential. Data analysis applies statistical analysis and logical techniques to describe, visualize, reduce, revise, summarize, and assess data into useful information that provides a better context for the data.

Multivariate regression has numerous applications in various areas. Let’s look at some examples to understand it better.

Praneeta wants to estimate the price of a house. She will collect details such as the location, number of bedrooms, size of square feet, amenities available, etc. Based on these details, she can predict the price of the house and how each variable is interrelated.

An agriculture scientist wants to predict the total crop yield expected for the summer. He collected details of the expected amount of rainfall, fertilizers to use, and soil conditions.By building a Multivariate regression model, scientists can predict crop yield. With the crop yield, the scientist also tries to understand the relationship among the variables.

Suppose an organization wants to know how much it has to pay a new hire. In that case, it will consider details such as education level, years of experience, job location, and whether the employee has niche skills. Based on this information, you can predict an employee’s salary, and these variables help estimate the salary.

Economists can use Multivariate regression to predict the GDP growth of a state or a country based on parameters such as the total amount spent by consumers, import expenditures, total gains from exports, and total savings.

A company wants to predict an apartment’s electricity bill. The details needed here are the number of flats, the number of appliances used, the number of people at home, etc. These variables can help predict the electricity bill.

The above example uses multivariate regression with many independent and single-dependent variables.

Check out the Statistical Analysis course to learn the statistical methods involved in data analysis.

Why perform Multivariate Regression Analysis?

Data analysis plays a significant role in finding meaningful information to help businesses make better decisions based on the output.

Along with Data analysis, Data science also comes into the picture. Data science combines many scientific methodologies, processes, algorithms, and tools to extract information, particularly massive datasets, for insights into structured and unstructured data.

A different range of terms related to data mining, cleaning, analyzing, and interpreting data are often used interchangeably in data science.

Let us look at one of the essential models of data science.

Regression analysis

Regression analysis is one of the most sought-after methods in data analysis. It is a supervised machine-learning algorithm. Regression analysis is an essential statistical method that allows us to examine the relationship between two or more variables in the dataset.

Regression analysis is a mathematical way of differentiating variables that impact output. It answers the question: What are the critical variables that impact output? Which ones should we ignore? How do they interact with each other?

We have a dependent variable—the main factor we try to understand or predict. Then, we have independent variables—the factors we believe impact the dependent variable.

Simple linear regression is a model that estimates the linear relationship between dependent and independent variables using a straight line.

On the other hand, Multiple linear regression estimates the relationship between two or more independent variables and one dependent variable. The difference between these two models is the number of independent variables influencing the result.

Sometimes, the regression models mentioned above will fail to work. Here’s why.

As known, regression analysis is mainly used to understand the relationship between a dependent and independent variable. However, there are ample situations in the real world where multiple independent variables influence the output.

Therefore, we have to look for other options rather than a single regression model that can only work with one independent variable.

With these setbacks in hand, we want a better model that will fill in the gaps of

Simple and multiple linear regression, and this is where Multivariate Linear Regression comes into the picture.

If you are a beginner in the field and wish to learn more such concepts to start your career in machine learning, you can head over to Great Learning Academy and learn the basics of machine learning, such as linear regression. The course will cover all the basic concepts required to kick-start your machine-learning journey.

Looking to improve your skills in regression analysis?

This regression analysis using Excel course will teach you all the techniques you need to know to get the most out of your data. You’ll learn how to build models, interpret results, and use regression analysis to make better decisions for your business.

Enroll today and get started on your path to becoming a data-driven decision-maker!

Mathematical equation

The simple regression linear model represents a straight line meaning y is a function of x. When we have an extra dimension (z), the straight line becomes a plane.

Here, the plane is the function that expresses y as a function of x and z. The linear regression equation can now be expressed as:

y = m1.x + m2.z+ c

y is the dependent variable, that is, the variable that needs to be predicted.
x is the first independent variable. It is the first input.

m1 is the slope of x1. It lets us know the angle of the line (x).
z is the second independent variable. It is the second input.
m2 is the slope of z. It helps us to know the angle of the line (z).
c is the intercept. A constant that finds the value of y when x and z are 0.

The equation for a model with two input variables can be written as:

y = β0 + β1.x1 + β2.x2

What if there are three variables as inputs? Human visualizations can be only three dimensions. In the machine learning world, there can be n number of dimensions. The equation for a model with three input variables can be written as:

y = β0 + β1.x1 + β2.x2 + β3.x3

Below is the generalized equation for the multivariate regression model-

y = β0 + β1.x1 + β2.x2 +….. + βn.xn

Where n represents the number of independent variables, β0~ βn represents the coefficients, and x1~xn is the independent variable.

The multivariate model helps us in understanding and comparing coefficients across the output. Here, the small cost function makes Multivariate linear regression a better model.

Also Read: 100+ Machine Learning Interview Questions

What is Cost Function?

The cost function is a function that allows a cost to samples when the model differs from observed data. This equation is the sum of the square of the difference between the predicted value and the actual value divided by twice the length of the dataset.

A smaller mean squared error implies better performance. Here, the cost is the sum of squared errors.

Cost of Multiple Linear regression:

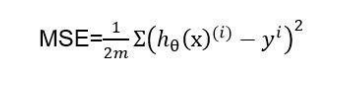
Steps of Multivariate Regression analysis

Multivariate Regression solves all the problems dealing with multiple independent and dependent variables. However, to build an accurate multivariate regression model, we’ll have to follow some steps:

Feature selection-
The selection of features is an important step in multivariate regression. Feature selection also known as variable selection. It becomes important for us to pick significant variables for better model building.
Normalizing Features-
We need to scale the features as it maintains general distribution and ratios in data. This will lead to an efficient analysis. The value of each feature can also be changed.
Select Loss function and Hypothesis-
The loss function predicts whenever there is an error. Meaning, when the hypothesis prediction deviates from actual values. Here, the hypothesis is the predicted value from the feature/variable.
Set Hypothesis Parameters-
The hypothesis parameter needs to be set in such a way that it reduces the loss function and predicts well.
Minimize the Loss Function-
The loss function needs to be minimized by using a loss minimization algorithm on the dataset, which will help in adjusting hypothesis parameters. After the loss is minimized, it can be used for further action. Gradient descent is one of the algorithms commonly used for loss minimization.
Test the hypothesis function-
The hypothesis function needs to be checked on as well, as it is predicting values. Once this is done, it has to be tested on test data.

Advantages of Multivariate Regression

Improved Predictive Accuracy: Multivariate regression can provide a more accurate and nuanced model than simple linear regression by incorporating multiple predictors.

Handles Complex Relationships: It can capture the relationships between the dependent variable and multiple predictors, including interactions and combined effects, leading to a better understanding of complex data structures.

Reduces Bias: Including several variables helps reduce bias by accounting for factors that might influence the dependent variable, leading to more reliable estimates.

Identifies Key Predictors: It helps determine which predictors significantly impact the outcome, aiding in feature selection and model refinement.

Improves Model Fit: Multivariate regression, by considering multiple variables, can often improve the fit of the model to the data, providing more detailed insights into the underlying relationships.

Disadvantages of Multivariate Regression

Multivariate regression analysis is complex and requires a high level of mathematical calculation.
The output produced by multivariate models is sometimes not accessible to interpret because it has some loss and error outputs that are not identical.
These models do not have much scope for smaller datasets. Hence, the same cannot be applied to them. The results are better for larger datasets.

Conclusion

Multivariate regression comes into the picture when we have more than one independent variable, and simple linear regression does not work. Real-world data involves multiple variables or features and when these are present in data, we would require Multivariate regression for better analysis.