- What is a Bayesian Network?
- What is Directed acyclic graph?
- Example of Bayesian Network
- Bayesian Network in Python
- Application of Bayesian Network
Contributed by: Rachit Jain
LinkedIn profile: https://www.linkedin.com/in/rachit-jain-37b63677/
The Bayesian network has given shape to most of the complex problems that provide less information and resources. It has been implemented in most of the advanced technologies like Artificial Intelligence and Machine learning.
What is a Bayesian Network?
A Bayesian network falls under the category of Probabilistic Graphical Modelling technique, which is used to calculate uncertainties by using the notion of probability.
They are used to model improbability using directed acyclic graphs.
What is Directed Acyclic Graph?
It is used to represent the Bayesian Network. A directed acyclic graph contains nodes and links, where links denote the relationship between nodes.
The node represents random variables and links define their relationship. In the diagram above, Node A and Node B are parents of Node C. This means, Node C is dependent on Node A and Node B. Likewise, Node D is the child of Node C and is dependent on Node C.
This graph can help in determining the uncertainty in an event occurring based on the conditional probability distribution of each random variable. A conditional probability table is used to represent this distribution of each variable in the network.
Let’s understand what conditional probability and joint probability are.
Joint Probability – It is the measure of two events happening at the same time. It can be written as P(A∩B)
Conditional Probability– It is the measure of the probability of an event occurring given that another event has occurred. In other terms, the conditional probability of an event X is the probability that the event will occur given that event Y has already occurred.
P(X|Y): Probability of event X occurring given that event Y already occurred.
If X and Y are dependent events, then P(X|Y) = P(X∩Y)/P(Y)
If X and Y are independent events, then P(X∩Y) = 0
So, P(X|Y) = P(X)
Let’s understand the Bayesian network by an example.
Example of Bayesian Network
In the above diagram, water spray and rain is the child of season, i.e., they are dependent on the season. If the floor is wet, then we can say there is rain. At last, if the floor is slippery, then it is wet.
So, we can say that the probability of a random variable is dependent on his parents.
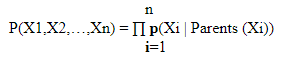
Bayesian Network in Python
Let’s write Python code on the famous Monty Hall Problem. The Monty Hall problem is a brain teaser, in the form of a probability puzzle, loosely based on the American television game show Let’s Make a Deal and named after its original host, Monty Hall.
Suppose you’re on a game show, and you’re given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what’s behind the doors, opens another door, say No. 3, which has a goat. He then says to you, “Do you want to pick door No. 2?” Is it to your advantage to switch your choice?
Let’s build a model.
#Import packages
import math
from pomegranate import *
# The door selected by the guest is totally random
guestSelection =DiscreteDistribution( { 'A': 1./3, 'B': 1./3, 'C': 1./3 } )
# The door having the prize is also a random process
prizeSelection =DiscreteDistribution( { 'A': 1./3, 'B': 1./3, 'C': 1./3 } )
# The door host Monty picks, depends on the choice of the guestSelection and the prizeSelection
montySelection =ConditionalProbabilityTable(
[[ 'A', 'A', 'A', 0.0 ],
[ 'A', 'A', 'B', 0.5 ],
[ 'A', 'A', 'C', 0.5 ],
[ 'A', 'B', 'A', 0.0 ],
[ 'A', 'B', 'B', 0.0 ],
[ 'A', 'B', 'C', 1.0 ],
[ 'A', 'C', 'A', 0.0 ],
[ 'A', 'C', 'B', 1.0 ],
[ 'A', 'C', 'C', 0.0 ],
[ 'B', 'A', 'A', 0.0 ],
[ 'B', 'A', 'B', 0.0 ],
[ 'B', 'A', 'C', 1.0 ],
[ 'B', 'B', 'A', 0.5 ],
[ 'B', 'B', 'B', 0.0 ],
[ 'B', 'B', 'C', 0.5 ],
[ 'B', 'C', 'A', 1.0 ],
[ 'B', 'C', 'B', 0.0 ],
[ 'B', 'C', 'C', 0.0 ],
[ 'C', 'A', 'A', 0.0 ],
[ 'C', 'A', 'B', 1.0 ],
[ 'C', 'A', 'C', 0.0 ],
[ 'C', 'B', 'A', 1.0 ],
[ 'C', 'B', 'B', 0.0 ],
[ 'C', 'B', 'C', 0.0 ],
[ 'C', 'C', 'A', 0.5 ],
[ 'C', 'C', 'B', 0.5 ],
[ 'C', 'C', 'C', 0.0 ]], [guestSelection, prizeSelection] )
d1 = State(guestSelection, name="guest choice" )
d2 = State(prizeSelection, name="prize choice" )
d3 = State(montySelection, name="monty choice" )
#Lets Building the Bayesian Network
network = BayesianNetwork(“Monty Hall Problem With Bayesian Networks”)
network.add_states(d1, d2, d3)
network.add_edge(d1, d3)
network.add_edge(d2, d3)
network.bake()
Here, A, B, C denotes the door picked by the guest, prize containing door, and Monty’s door.
Let’s make the predictions assuming guest picks A. Monty is going to pick up either B or C as A contains a prize.
beliefs = network.predict_proba({ 'guestSelection' : 'A' })
beliefs = map(str, beliefs)
print("n".join( "{}t{}".format( state.name, belief ) for state, belief in zip( network.states, beliefs ) ))
guest A
prize {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"A" :0.3333333333333333,
"B" :0.3333333333333333,
"C" :0.3333333333333333
}
],
}
monty {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"C" :0.49999999999999983,
"A" :0.0,
"B" :0.49999999999999983
}
],
}
beliefs = network.predict_proba({'guestSelection' : 'A', 'montySelection' : 'B'})
print("n".join( "{}t{}".format( state.name, str(belief) ) for state, belief in zip( network.states, beliefs )))
guest A
prize {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"A" :0.3333333333333334,
"B" :0.0,
"C" :0.6666666666666664
}
],
}
monty B
Here, guests select door A and Monty selects door B, and we can see the probability of moving from door A to door C is given as 0.66.
Guests who switched the door, then their chances of winning are 66% and the guest who did not switch the door is 33%.
Also Read: An Introduction to Naive Bayes
Application of Bayesian Network
Healthcare Industry: The Bayesian network is used in the healthcare industry for the detection and prevention of diseases. Based on models built, we can find out the likely symptoms and predict whether a person will be diseased or not. For instance, if a person has cholesterol, then there are high chances that the person gets a heart problem. With this information, a person can take preventive measures.
Web Search: Bayesian Network modes can be used for search accuracy based on user intent. Based on the user’s intent, these models show things that are relevant to the person. For instance, when we search for Python functions most of the time, then the web search model activates our intent and it makes sure to show relevant things to the user.
Mail Spam Filtering: Gmail is using Bayesian Models to filter the mails by reading or understanding the context of mail. For instance, we may have observed spam emails in the spam folder in Gmail. So, how are these emails classified as spams? Using the Bayesian model, which observes the mail and based on the previous experience and the probability it classifies mail as spam or not.
Biomonitoring: Bayesian Models are used to quantify the concentration of chemicals in blood and human tissues. These use indicators to measure blood and urine. To find the level of ECCs, one can conduct biometric studies.
Information Retrieval: Models can be used for retrieving information from the database. During this process, we refine our problem multiple times. It is used to reduce information overload.
If you wish to learn more concepts related to Artificial Intelligence and Machine Learning, upskill with Great Learning’s PG program in Artificial Intelligence and Machine Learning.






