Introduction to Hypothesis Testing in R Case Studies, Concept and Examples

– By Dr. Masood H. Siddiqui, Professor & Dean (Research) at Jaipuria Institute of Management, Lucknow

Introduction to Hypothesis Testing in R

The premise of Data Analytics is based on the philosophy of the “Data-Driven Decision Making” that univocally states that decision-making based on data has less probability of error than those based on subjective judgement and gut-feeling. So, we require data to make decisions and to answer the business/functional questions. Data may be collected from each and every unit/person, connected with the problem-situation (totality related to the situation). This is known as Census or Complete Enumeration and the ‘totality’ is known as Population. Obv.iously, this will generally give the most optimum results with maximum correctness but this may not be always possible. Actually, it is rare to have access to information from all the members connected with the situation. So, due to practical considerations, we take up a representative subset from the population, known as Sample. A sample is a representative in the sense that it is expected to exhibit the properties of the population, from where it has been drawn.

So, we have evidence (data) from the sample and we need to decide for the population on the basis of that data from the sample i.e. inferring about the population on the basis of a sample. This concept is known as Statistical Inference.

Before going into details, we should be clear about certain terms and concepts that will be useful:

Parameter and Statistic

Parameters are unknown constants that effectively define the population distribution, and in turn, the population, e.g. population mean (µ), population standard deviation (σ), population proportion (P) etc. Statistics are the values characterising the sample i.e. characteristics of the sample. They are actually functions of sample values e. g. sample mean (x̄), sample standard deviation (s), sample proportion (p) etc.

Sampling Distribution

A large number of samples may be drawn from a population. Each sample may provide a value of sample statistic, so there will be a distribution of sample statistic value from all the possible samples i.e. frequency distribution of sample statistic. This is better known as Sampling distribution of the sample statistic. Alternatively, the sample statistic is a random variable, being a function of sample values (which are random variables themselves). The probability distribution of the sample statistic is known as sampling distribution of sample statistic. Just like any other distribution, sampling distribution may partially be described by its mean and standard deviation. The standard deviation of sampling distribution of a sample statistic is better known as the Standard Error of the sample statistic.

Standard Error

It is a measure of the extent of variation among different values of statistics from different possible samples. Higher the standard error, higher is the variation among different possible values of statistics. Hence, less will be the confidence that we may place on the value of the statistic for estimation purposes. Hence, the sample statistic having a lower value of standard error is supposed to be better for estimation of the population parameter.

Example:

1(a). A sample of size ‘n’ has been drawn for a normal population N (µ, σ). We are considering sample mean (x̄) as the sample statistic. Then, the sampling distribution of sample statistic x̄ will follow Normal Distribution with mean µ_x̄ = µ and standard error σ_x̄ = σ/√n.

Even if the population is not following the Normal Distribution but for a large sample (n = large), the sampling distribution of x̄ will approach to (approximated by) normal distribution with mean µ_x̄ = µ and standard error σ_x̄ = σ/√n, as per the Central Limit Theorem.

(b). A sample of size ‘n’ has been drawn for a normal population N (µ, σ), but population standard deviation σ is unknown, so in this case σ will be estimated by sample standard deviation(s). Then, sampling distribution of sample statistic x̄ will follow the student’s t distribution (with degree of freedom = n-1) having mean µ_x̄ = µ and standard error σ_x̄ = s/√n.

2. When we consider proportions for categorical data. Sampling distribution of sample proportion p =x/n (where x = Number of success out of a total of n) will follow Normal Distribution with mean µ_p = P and standard error σ_p = √(PQ/n), (where Q = 1-P). This is under the condition that n is large such that both np and nq should be minimum 5.

Statistical Inference

Statistical Inference encompasses two different but related problems:

1. Knowing about the population-values on the basis of data from the sample. This is known as the problem of Estimation. This is a common problem in business decision-making because of lack of complete information and uncertainty but by using sample information, the estimate will be based on the concept of data based decision making. Here, the concept of probability is used through sampling distribution to deal with the uncertainty. If sample statistics is used to estimate the population parameter, then in that situation that is known as the Estimator; {like sample mean (x̄) to estimate population mean µ, sample proportion (p) to estimate population proportion (P) etc.}. A particular value of the estimator for a given sample is known as Estimate. For example, if we want to estimate average sales of 1000+ outlets of a retail chain and we have taken a sample of 40 outlets and sample mean (estimator) x̄ is 40000. Then the estimate will be 40000.

There are two types of estimation:

Point Estimation: Single value/number of the estimator is used to estimate unknown population parameters. The example is given above.
Confidence Interval/Interval Estimation: Interval Estimate gives two values of sample statistic/estimator, forming an interval or range, within which an unknown population is expected to lie. This interval estimate provides confidence with the interval vis-à-vis the population parameter. For example: 95% confidence interval for population mean sale is (35000, 45000) i.e. we are 95% confident that interval estimate will contain the population parameter.

2. Examining the declaration/perception/claim about the population for its correctness on the basis of sample data. This is known as the problem of Significant Testing or Testing of Hypothesis. This belongs to the Confirmatory Data Analysis, as to confirm or otherwise the hypothesis developed in the earlier Exploratory Data Analysis stage.

Testing of Hypothesis in R

One Sample Tests

z-test – Hypothesis Testing of Population Mean when Population Standard Deviation is known:

Hypothesis testing in R starts with a claim or perception of the population. Hypothesis may be defined as a claim/ positive declaration/ conjecture about the population parameter. If hypothesis defines the distribution completely, it is known as Simple Hypothesis, otherwise Composite Hypothesis.

Hypothesis may be classified as:

Null Hypothesis (H₀): Hypothesis to be tested is known as Null Hypothesis (H₀). It is so known because it assumes no relationship or no difference from the hypothesized value of population parameter(s) or to be nullified.

Alternative Hypothesis (H₁): The hypothesis opposite/complementary to the Null Hypothesis.

Note: Here, two points are needed to be considered. First, both the hypotheses are to be constructed only for the population parameters. Second, since H₀is to be tested so it is H₀only that may be rejected or failed to be rejected (retained).

Hypothesis Testing: Hypothesis testing a rule or statistical process that may be resulted in either rejecting or failing to reject the null hypothesis (H₀).

The Five Steps Process of Hypothesis Testing

Here, we take an example of Testing of Mean:

1. Setting up the Hypothesis:

This step is used to define the problem after considering the business situation and deciding the relevant hypotheses H₀ and H₁, after mentioning the hypotheses in the business language.

We are considering the random variable X = Quarterly sales of the sales executive working in a big FMCG company. Here, we assume that sales follow normal distribution with mean µ (unknown) and standard deviation σ (known). The value of the population parameter (population mean) to be tested be µ₀(Hypothesised Value).

Here the hypothesis may be:

H₀: µ = µ₀or µ ≤ µ₀or µ ≥ µ₀ (here, the first one is Simple Hypothesis, rest two variants are composite hypotheses)

H₁: µ > µ₀or

H₁: µ < µ₀or

H₁: µ ≠ µ₀

(Here, all three variants are Composite Hypothesis)

2. Defining Test and Test Statistic:

The test is the statistical rule/process of deciding to ‘reject’ or ‘fail to reject’ (retain) the H0. It consists of dividing the sample space (the totality of all the possible outcomes) into two complementary parts. One part, providing the rejection of H₀, known as Critical Region. The other part, representing the failing to reject H₀situation, is known as Acceptance Region.

The logic is, since we have evidence only from the sample, we use sample data to decide about the rejection/retaining of the hypothesised value. Sample, in principle, can never be a perfect replica of the population so we do expect that there will be variation in between population and sample values. So the issue is not the difference but actually the magnitude of difference. Suppose, we want to test the claim that the average quarterly sale of the executive is 75k vs sale is below 75k. Here, the hypothesised value for the population mean is µ₀=75 i.e.

H₀: µ = 75

H₁: µ < 75.

Suppose from a sample, we get a value of sample mean x̄=73. Here, the difference is too small to reject the claim under H₀since the chances (probability) of happening of such a random sample is quite large so we will retain H₀. Suppose, in some other situation, we get a sample with a sample mean x̄=33. Here, the difference between the sample mean and hypothesised population mean is too large. So the claim under H₀ may be rejected as the chance of having such a sample for this population is quite low.

So, there must be some dividing value (s) that differentiates between the two decisions: rejection (critical region) and retention (acceptance region), this boundary value is known as the critical value.

Type I and Type II Error:

There are two types of situations (H₀is true or false) which are complementary to each other and two types of complementary decisions (Reject H₀ or Failing to Reject H₀). So we have four types of cases:

	H₀is True	H₀is False
Reject H₀	Type I Error	Correct Decision
Fails to Reject H₀	Correct Decision	Type II Error

So, the two possible errors in hypothesis testing can be:

Type I Error = [Reject H₀ when H₀ is true]

Type II Error = [Fails to reject H₀when H₀is false].

Type I Error is also known as False Positive and Type II Error is also known as False Negative in the language of Business Analytics.

Since these two are probabilistic events, so we measure them using probabilities:

α = Probability of committing Type I error = P [Reject H₀ / H₀ is true]

β = Probability of committing Type II error = P [Fails to reject H₀/ H₀is false].

For a good testing procedure, both types of errors should be low (minimise α and β) but simultaneous minimisation of both the errors is not possible because they are interconnected. If we minimize one, the other will increase and vice versa. So, one error is fixed and another is tried to be minimised. Normally α is fixed and we try to minimise β. If Type I error is critical, α is fixed at a low value (allowing β to take relatively high value) otherwise at relatively high value (to minimise β to a low value, Type II error being critical).

Example: In Indian Judicial System we have H₀: Under trial is innocent. Here, Type I Error = An innocent person is sentenced, while Type II Error = A guilty person is set free. Indian (Anglo Saxon) Judicial System considers type I error to be critical so it will have low α for this case.

Power of the test = 1- β = P [Reject H₀/ H₀is false].

Higher the power of the test, better it is considered and we look for the Most Powerful Test since power of test can be taken as the probability that the test will detect a deviation from H₀ given that the deviation exists.

One Tailed and Two Tailed Tests of Hypothesis:

Case I:

H₀: µ ≤ µ₀

H₁: µ > µ₀

When x̄ is significantly above the hypothesized population mean µ₀ then H₀ will be rejected and the test used will be right tailed test (upper tailed test) since the critical region (denoting rejection of H₀ will be in the right tail of the normal curve (representing sampling distribution of sample statistic x̄). (The critical region is shown as a shaded portion in the figure).

Case II:

H₀: µ ≥ µ₀

H₁: µ < µ₀

Inthis case, if x̄ is significantly below the hypothesised population mean µ₀ then H₀ will be rejected and the test used will be the left tailed test (lower tailed test) since the critical region (denoting rejection of H₀) will be in the left tail of the normal curve (representing sampling distribution of sample statistic x̄). (The critical region is shown as a shaded portion in the figure).

These two tests are also known as One-tailed tests as there will be a critical region in only one tail of the sampling distribution.

Case III:

H₀: µ = µ₀

H₁: µ ≠ µ₀

When x̄ is significantly different (significantly higher or lower than) from the hypothesised population mean µ₀, then H₀ will be rejected. Inthis case, the two tailed test will be applicable because there will be two critical regions (denoting rejection of H₀) on both the tails of the normal curve (representing sampling distribution of sample statistic x̄). (The critical regions are shown as shaded portions in the figure).

Hypothesis Testing using Standardized Scale: Here, instead of measuring sample statistic (variable) in the original unit, standardised value is taken (better known as test statistic). So, the comparison will be between observed value of test statistic (estimated from sample), and critical value of test statistic (obtained from relevant theoretical probability distribution).

Here, since population standard deviation (σ) is known, so the test statistics:

Z= (x- µx̄_x)/σ x̄ = (x- µ₀)/(σ/√n) follows Standard Normal Distribution N (0, 1).

3.Deciding the Criteria for Rejection or otherwise:

As discussed, hypothesis testing means deciding a rule for rejection/retention of H₀. Here, the critical region decides rejection of H₀and there will be a value, known as Critical Value, to define the boundary of the critical region/acceptance region. The size (probability/area) of a critical region is taken as α. Here, α may be known as Significance Level, the level at which hypothesis testing is performed. It is equal to type I error, as discussed earlier.

Suppose, α has been decided as 5%, so the critical value of test statistic (Z) will be +1.645 (for right tail test), -1.645 (for left tail test). For the two tails test, the critical value will be -1.96 and +1.96 (as per the Standard Normal Distribution Z table). The value of α may be chosen as per the criticality of type I and type II. Normally, the value of α is taken as 5% in most of the analytical situations (Fisher, 1956).

4. Taking sample, data collection and estimating the observed value of test statistic:

In this stage, a proper sample of size n is taken and after collecting the data, the values of sample mean (x̄) and the observed value of test statistic Z_obs is being estimated, as per the test statistic formula.

5. Taking the Decision to reject or otherwise:

On comparing the observed value of Test statistic with that of the critical value, we may identify whether the observed value lies in the critical region (reject H₀) or in the acceptance region (do not reject H₀) and decide accordingly.

Right Tailed Test: If Z_obs > 1.645 : Reject H₀ at 5% Level of Significance.
Left Tailed Test: If Z_obs < -1.645 : Reject H₀ at 5% Level of Significance.
Two Tailed Test: If Z_obs > 1.96 or If Z_obs < -1.96 : Reject H₀ at 5% Level of Significance.

p-value: An Alternative way of Hypothesis Testing:

There is an alternative approach for hypothesis testing, this approach is very much used in all the software packages. It is known as probability value/ prob. value/ p-value. It gives the probability of getting a value of statistic this far or farther from the hypothesised value if H0 is true. This denotes how likely is the result that we have observed. It may be further explained as the probability of observing the test statistic if H₀is true i.e. what are the chances in support of occurrence of H₀. If p-value is small, it means there are less chances (rare case) in favour of H₀ occuring, as the difference between a sample value and hypothesised value is significantly large so H₀may be rejected, otherwise it may be retained.

If p-value < α : Reject H₀

If p-value ≥ α : Fails to Reject H₀

So, it may be mentioned that the level of significance (α) is the maximum threshold for p-value. It should be noted that p-value (two tailed test) = 2* p-value (one tailed test).

Note: Though the application of z-test requires the ‘Normality Assumption’ for the parent population with known standard deviation/ variance but if sample is large (n>30), the normality assumption for the parent population may be relaxed, provided population standard deviation/variance is known (as per Central Limit Theorem).

t-test: Hypothesis Testing of Population Mean when Population Standard Deviation is Unknown:

As we discussed in the previous case, for testing of population mean, we assume that sample has been drawn from the population following normal distribution mean µ and standard deviation σ. In this case test statistic Z = (x- µ₀)/(σ/√n) ~ Standard Normal Distribution N (0, 1). But in the situations where population s.d. σ is not known (it is a very common situation in all the real life business situations), we estimate population s.d. (σ) by sample s.d. (s).

Hence the corresponding test statistic:

t= (x- µx̄_x)/σ x̄ = (x- µ₀)/(s/√n) follows Student’s t distribution with (n-1) degrees of freedom. One degree of freedom has been sacrificed for estimating population s.d. (σ) by sample s.d. (s).

Everything else in the testing process remains the same.

t-test is not much affected if assumption of normality is violated provided data is slightly asymmetrical (near to symmetry) and data-set does not contain outliers.

t-distribution:

The Student’s t-distribution, is much similar to the normal distribution. It is a symmetric distribution (bell shaped distribution). In general Student’s t distribution is flatter i.e. having heavier tails. Shape of t distribution changes with degrees of freedom (exact distribution) and becomes approximately close to Normal distribution for large n.

Two Samples Tests: Hypothesis Testing for the difference between two population means

In many business decision making situations, decision makers are interested in comparison of two populations i.e. interested in examining the difference between two population parameters. Example: comparing sales of rural and urban outlets, comparing sales before the advertisement and after advertisement, comparison of salaries in between male and female employees, comparison of salary before and after joining the data science courses etc.

Independent Samples and Dependent (Paired Samples):

Depending on method of collection data for the two samples, samples may be termed as independent or dependent samples. If two samples are drawn independently without any relation (may be from different units/respondents in the two samples), then it is said that samples are drawn independently. If samples are related or paired or having two observations at different points of time on the same unit/respondent, then the samples are said to be dependent or paired. This approach (paired samples) enables us to compare two populations after controlling the extraneous effect on them.

Testing the Difference Between Means: Independent Samples

Two Samples Z Test:

We have two populations, both following Normal populations as N (µ₁, σ₁) and N (µ₂, σ₂). We want to test the Null Hypothesis:

H₀: µ₁– µ₂= θ or µ₁– µ₂≤ θ or µ₁– µ₂≥ θ

Alternative hypothesis:

H₁: µ₁– µ₂> θ or

H₀: µ₁– µ₂< θ or

H₁: µ₁– µ₂≠ θ

(where θ may take any value as per the situation or θ =0).

Two samples of size n₁ and n₂ have been taken randomly from the two normal populations respectively and the corresponding sample means are x̄₁ and x̄₂.

Here, we are not interested in individual population parameters (means) but in the difference of population means (µ₁– µ₂). So, the corresponding statistic is = (x̄₁ – x̄₂).

According, sampling distribution of the statistic (x̄₁ – x̄₂) will follow Normal distribution with mean µ_x̄ = µ₁– µ₂ and standard error σ_x̄= √ (σ²₁/ n₁+ σ²₂/ n₂). So, the corresponding Test Statistics will be:

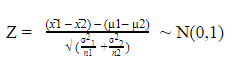
Other things remaining the same as per the One Sample Tests (as explained earlier).

Two Independent Samples t-Test (when Population Standard Deviations are Unknown):

Here, for testing the difference of two population mean, we assume that samples have been drawn from populations following Normal Distributions, but it is a very common situation that population standard deviations (σ₁ and σ₂) are unknown. So they are estimated by sample standard deviations (s₁ and s₂) from the respective two samples.

Here, two situations are possible:

(a) Population Standard Deviations are unknown but equal:

In this situation (where σ₁ and σ₂are unknown but assumed to be equal), sampling distribution of the statistic (x̄₁ – x̄₂) will follow Student’s t distribution with mean µ_x̄ = µ₁– µ₂ and standard error σ_x̄= √ Sp²(1/ n₁+ 1/ n₂). Where Sp² is the pooled estimate, given by:

Sp² = (n₁-1) S₁²+(n₂-1) S₂²/(n₁+n₂-2)

So, the corresponding Test Statistics will be:

t = {(x̄₁ – x̄₂) – (µ₁– µ₂)}/{√ Sp²(1/n₁+1/n₂)}

Here, t statistic will follow t distribution with d.f. (n₁+n₂-2).

(b) Population Standard Deviations are unknown but unequal:

In this situation (where σ₁ and σ₂are unknown and unequal).

Then the sampling distribution of the statistic (x̄₁ – x̄₂) will follow Student’s t distribution with mean µ_x̄ = µ₁– µ₂ and standard error Se=√ (s²₁/ n₁+ s²₂/ n₂).

So, the corresponding Test Statistics will be:

t = {(x̄₁ – x̄₂) – (µ₁– µ₂)}/{√ (s2₁/n₁+s2₂/n₂)}

The test statistic will follow Student’s t distribution with degrees of freedom (rounding down to nearest integers):

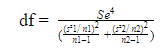
Hypothesis Testing for Equality of Population Variances

As discussed in the aforementioned two cases, it is important to figure out whether the two population variances are equal or otherwise. For this purpose, F test can be employed as:

H₀: σ²₁ = σ²₂and H₁: σ²₁ ≠ σ²₂

Two samples of sizes n₁ and n₂ have been drawn from two populations respectively. They provide sample standard deviations s₁ and s₂. The test statistic is F = s₁²/s₂²

The test statistic will follow F-distribution with (n₁-1) df for numerator and (n₂-1) df for denominator.

Note: There are many other tests that are applied for this purpose.

Paired Sample t-Test (Testing Difference between Means with Dependent Samples):

As discussed earlier, in the situation of Before-After Tests, to examine the impact of any intervention like a training program, health program, any campaign to change status, we have two set of observations (x_iand y_i) on the same test unit (respondent or units) before and after the program. Each sample has “n” paired observations. The Samples are said to be dependent or paired.

Here, we consider a random variable: d_i= x_i– y_i.

Accordingly, the sampling distribution of the sample statistic (sample mean of the differentces d_i’s) will follow Student’s t distribution with mean = θ and standard error = sd/√n, where sd is the sample standard deviation of d_i’s.

Hence, the corresponding test statistic: t = (d̅- θ)/sd/√n will follow t distribution with (n-1).

As we have observed, paired t-test is actually one sample test since two samples got converted into one sample of differences. If ‘Two Independent Samples t-Test’ and ‘Paired t-test’ are applied on the same data set then two tests will give much different results because in case of Paired t-Test, standard error will be quite low as compared to Two Independent Samples t-Test. The Paired t-Test is applied essentially on one sample while the earlier one is applied on two samples. The result of the difference in standard error is that t-statistic will take larger value in case of ‘Paired t-Test’ in comparison to the ‘Two Independent Samples t-Test and finally p-values get affected accordingly.

t-Test in SPSS:

One Sample t-test

Analyze => Compare Means=> One-Sample T-Test to open relevant dialogue box.

Test variable (variable under consideration) in the Test variable(s) box and hypothesised value µ₀= 75 (for example) in the Test Value box are to be entered.

Press Ok to have the output.

Here, we consider the example of Ventura Sales, and want to examine the perception that average sales in the first quarter is 75 (thousand) vs it is not. So, the Hypotheses:

Null Hypothesis H₀: µ=75

Alternative Hypothesis H₁: µ≠75

T-Test

One-Sample Statistics

	N	Mean	Std. Deviation	Std. Error Mean
Sale of the outlet in 1st Quarter(Rs.’000)	60	72.02	9.724	1.255

Descriptive table showing the sample size n = 60, sample mean x̄=72.02, sample sd s=9.724.

One-Sample Test

One Sample Test Table shows the result of the t-test. Here, test statistic value (from the sample) is t = -2.376 and the corresponding p-value (2 tailed) = 0.021 <0.05. So, H₀ got rejected and it can be said that the claim of average first quarterly sales being 75 (thousand) does not hold.

Two Independent Samples t-Test

Analyze => Compare Means=> Independent-Samples T-Test to open the dialogue box.
Enter the Test variable (variable under consideration) in the Test Variable(s) box and variable categorising the groups in the Grouping Variable box.

Define the groups by clicking on Define Groups and enter the relevant numeric-codes into the relevant groups in the Define Groups sub-dialogue box. Press Continue to return back to the main dialogue box.

Press Ok to have the output.

We continue with the example of Ventura Sales, and want to compare the average first quarter sales with respect to Urban Outlets and Rural Outlets (two independent samples/groups). Here, the claim is that urban outlets are giving lower sales as compared to rural outlets. So, the Hypotheses:

H₀: µ₁– µ₂= 0 or µ₁= µ₂ (Where, µ₁= Population Mean Sale of Urban Outlets and µ₂= Population Mean Sale of Rural Outlets)

Alternative hypothesis:

H₁: µ₁< µ₂

Group Statistics

	Type of Outlet	N	Mean	Std. Deviation	Std. Error Mean
Sale of the outlet in 1st Quarter(Rs.’000)	Urban Outlet	37	67.86	8.570	1.409
Rural Outlet	Rural Outlet	23	78.70	7.600	1.585

Descriptive table showing the sample sizes n₁=37 and n₂=23, sample means x̄₁=67.86 and x̄₂=78.70, sample standard deviations s₁=8.570 and s₂= 7.600.

The below table is the Independent Sample Test Table, proving all the relevant test statistics and p-values. Here, both the outputs for Equal Variance (assumed) and Unequal Variance (assumed) are presented.

Independent Samples Test

So, we have to figure out whether we should go for ‘equal variance’ case or for ‘unequal variances’ case.

Here, Levene’s Test for Equality of Variances has to be applied for this purpose with the hypotheses: H₀: σ²₁ = σ²₂and H₁: σ²₁ ≠ σ²₂. The p-value (Sig) = 0.460 >0.05, so we can’t reject (so retained) H₀. Hence, variances can be assumed to be equal.

So, “Equal Variances assumed” case is to be taken up. Accordingly, the value of t statistic = -4.965 and the p-value (two tailed) = 0.000, so the p-value (one tailed) = 0.000/2 = 0.000 <0.05. Hence, H₀ got rejected and it can be said that urban outlets are giving lower sales in the first quarter. So, the claim stands.

Paired t-Test (Testing Difference between Means with Dependent Samples):

Analyze => Compare Means=> Paired-Samples T-Test to open the dialogue box.

Enter the relevant pair of variables (paired samples) in the Paired Variables box.

After entering the paired samples, press Ok to have the output.

We continue with the example of Ventura Sales, and want to compare the average first quarter sales with the second quarter sales. Some sales promotion interventions were executed with an expectation of increasing sales in the second quarter. So, the Hypotheses:

H₀: µ₁= µ₂ (Where, µ₁= Population Mean Sale of Quarter-I and µ₂= Population Mean Sale of Quarter-II)

Alternative hypothesis:

H₁: µ₁< µ₂ (representing the increase of sales i.e. implying the success of sales interventions)

Paired Samples Statistics

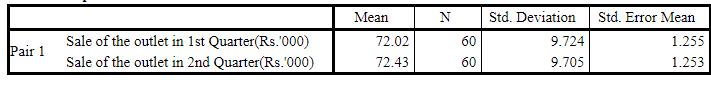
Descriptive table showing the sample size n=60, sample means x̄₁=72.02 and x̄₂=72.43.

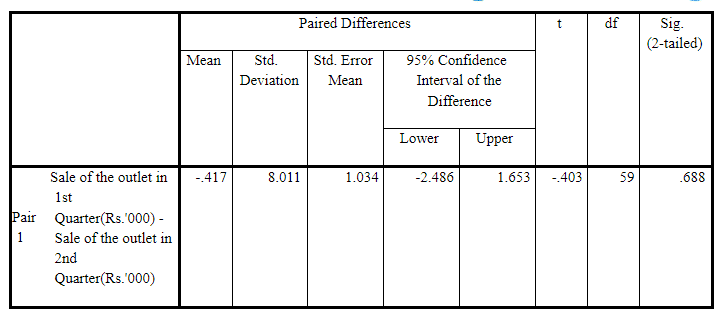
As per the following output table (Paired Samples Test), sample mean of differences d̅ = -0.417 with standard deviation of differences sd = 8.011 and value of t statistic = -0.403. Accordingly, the p-value (two tailed) = 0.688, so the p-value (one tailed) = 0.688/2 = 0.344 > 0.05. So, there have not been sufficient reasons to Reject H₀ i.e. H₀ should be retained. So, the effectiveness (success) of the sales promotion interventions is doubtful i.e. it didn’t result in significant increase in sales, provided all other extraneous factors remain the same.

Paired Samples Test

Let’s Look at some Case studies:

t-Test Application One Sample

Experience Marketing Services reported that the typical American spends a mean of 144 minutes (2.4 hours) per day accessing the Internet via a mobile device. (Source: The 2014 Digital Marketer, available at ex.pn/1kXJifX.) To test the validity of this statement, you select a sample of 30 friends and family. The result for the time spent per day accessing the Internet via a mobile device (in minutes) are stored in Internet_Mobile_Time.csv file.

Is there evidence that the populations mean time spent per day accessing the Internet via a mobile device is different from 144 minutes? Use the p-value approach and a level of significance of 0.05

What assumption about the population distribution is needed to conduct the test in A?

Solution In R

>setwd("D:/Hypothesis")
> Mydata=read.csv("InternetMobileTime.csv", header = TRUE)

> attach(mydata)
> xbar=mean(Minutes)
> s=sd(Minutes)
> n=length(Minutes)
> Mu=144 #null hypothesis
> tstat=(xbar-Mu)/(s/(n^0.5))
> tstat

[1] 1.224674

> Pvalue=2*pt(tstat, df=n-1, lower=FALSE)
> Pvalue

[1] 0.2305533

> if(Pvalue<0.05)NullHypothesis else "Accepted"

[1] “Accepted”

Independent t-test two sample

A hotel manager looks to enhance the initial impressions that hotel guests have when they check-in. Contributing to initial impressions is the time it takes to deliver a guest’s luggage to the room after check-in. A random sample of 20 deliveries on a particular day was selected each from Wing A and Wing B of the hotel. The data collated is given in Luggage.csv file. Analyze the data and determine whether there is a difference in the mean delivery times in the two wings of the hotel. (use alpha = 0.05).

Solution In R

> t.test(WingA,WingB, var.equal = TRUE, alternative = "greater")

Two Sample t-test
data: WingA and WingB
t = 5.1615,
df = 38,
p-value = 4.004e-06
alternative hypothesis: true difference in means is greater than 0
95 percent confidence interval:
1.531895 Inf
sample estimates:
mean of x mean of y
10.3975 8.1225
> t.test(WingA,WingB)
Welch Two Sample t-test

data:  WingA and WingB

t = 5.1615, df = 37.957, p-value = 8.031e-06
alternative hypothesis: true difference in means is not equal to 0
95 per cent confidence interval:
1.38269 3.16731
sample estimates:
mean of x mean of y
10.3975 8.1225

boxplot(WingA,WingB, col = c("Red","Pink"), horizontal = TRUE)

Case Study- Titan Insurance Company

The Titan Insurance Company has just installed a new incentive payment scheme for its lift policy salesforce. It wants to have an early view of the success or failure of the new scheme. Indications are that the sales force is selling more policies, but sales always vary in an unpredictable pattern from month to month and it is not clear that the scheme has made a significant difference.

Life Insurance companies typically measure the monthly output of a salesperson as the total sum assured for the policies sold by that person during the month. For example, suppose salesperson X has, in the month, sold seven policies for which the sums assured are £1000, £2500, £3000, £5000, £10000, £35000. X’s output for the month is the total of these sums assured, £61,500.

Titan’s new scheme is that the sales force receives low regular salaries but are paid large bonuses related to their output (i.e. to the total sum assured of policies sold by them). The scheme is expensive for the company, but they are looking for sales increases which more than compensate. The agreement with the sales force is that if the scheme does not at least break even for the company, it will be abandoned after six months.

The scheme has now been in operation for four months. It has settled down after fluctuations in the first two months due to the changeover.

To test the effectiveness of the scheme, Titan has taken a random sample of 30 salespeople measured their output in the penultimate month before changeover and then measured it in the fourth month after the changeover (they have deliberately chosen months not too close to the changeover). Table 1 shows the outputs of the salespeople in Table 1

SALESPERSON	Old_Scheme	New_Scheme
1	57	62
2	103	122
3	59	54
4	75	82
5	84	84
6	73	86
7	35	32
8	110	104
9	44	38
10	82	107
11	67	84
12	64	85
13	78	99
14	53	39
15	41	34
16	39	58
17	80	73
18	87	53
19	73	66
20	65	78
21	28	41
22	62	71
23	49	38
24	84	95
25	63	81
26	77	58
27	67	75
28	101	94
29	91	100
30	50	68

Data preparation

Since the given data are in 000, it will be better to convert them in thousands.

Problem 1
Describe the five per cent significance test you would apply to these data to determine whether the new scheme has significantly raised outputs? What conclusion does the test lead to?
Solution:
It is asked that whether the new scheme has significantly raised the output, it is an example of the one-tailed t-test.
Note: Two-tailed test could have been used if it was asked “new scheme has significantly changed the output”
Mean of amount assured before the introduction of scheme = 68450
Mean of amount assured after the introduction of scheme = 72000
Difference in mean = 72000 – 68450 = 3550
Let,
μ1 = Average sums assured by salesperson BEFORE changeover. μ2 = Average sums assured by salesperson AFTER changeover.
H0: μ1 = μ2 ; μ2 – μ1 = 0
HA: μ1 < μ2 ; μ2 – μ1 > 0 ; true difference of means is greater than zero.
Since population standard deviation is unknown, paired sample t-test will be used.

Since p-value (=0.06529) is higher than 0.05, we accept (fail to reject) NULL hypothesis. The new scheme has NOT significantly raised outputs.

Problem 2
Suppose it has been calculated that for Titan to break even, the average output must increase by £5000. If this figure is an alternative hypothesis, what is:
(a) The probability of a type 1 error?
(b) What is the p-value of the hypothesis test if we test for a difference of $5000?
(c) Power of the test:
Solution:
2.a. The probability of a type 1 error?
Solution: Probability of Type I error = significant level = 0.05 or 5%
2.b. What is the p-value of the hypothesis test if we test for a difference of $5000?
Solution:
Let μ2 = Average sums assured by salesperson AFTER changeover.
μ1 = Average sums assured by salesperson BEFORE changeover.
μd = μ2 – μ1 H0: μd ≤ 5000 HA: μd > 5000
This is a right tail test.

R code:

P-value = 0.6499
2.c. Power of the test.
Solution:
Let μ2 = Average sums assured by salesperson AFTER changeover. μ1 = Average sums assured by salesperson BEFORE changeover. μd = μ2 – μ1 H0: μd = 4000
HA: μd > 0

H0 will be rejected if test statistics > t_critical.
With α = 0.05 and df = 29, critical value for t statistic (or t_critical ) will be 1.699127.
Hence, H0 will be rejected for test statistics ≥ 1.699127.
Hence, H0 will be rejected if for 𝑥̅ ≥ 4368.176

R Code:

      Probability (type II error) is P(Do not reject H0 | H0 is false)
      Our NULL hypothesis is TRUE at μd = 0 so that H0: μd = 0 ; HA: μd > 0
      Probability of type II error at μd = 5000

= P (Do not reject H0 | H0 is false)
= P (Do not reject H0 | μd = 5000) = P (𝑥̅ < 4368.176 | μd = 5000)
= P (t < | μd = 5000)
= P (t < -0.245766)
= 0.4037973

R Code:
Now, β=0.5934752,
Power of test = 1- β = 1- 0.5934752
= 0.4065248

Note:

While performing Hypothesis-Testing, Hypotheses can’t be proved or disproved since we have evidence from sample (s) only. At most, Hypotheses may be rejected or retained.
Use of the term “accept H₀” in place of “do not reject” should be avoided even if the test statistic falls in the Acceptance Region or p-value ≥ α. This simply means that the sample does not provide sufficient statistical evidence to reject the H₀. Since we have tried to nullify (reject) H₀but we haven’t found sufficient support to do so, we may retain it but it won’t be accepted.
Confidence Interval (Interval Estimation) can also be used for testing of hypotheses. If the hypothesis parameter falls within the confidence interval, we do not reject H₀. Otherwise, if the hypothesised parameter falls outside the confidence interval i.e. confidence interval does not contain the hypothesized parameter, we reject H₀.

References:

Downey, A. B. (2014). Think Stat: Exploratory Data Analysis, 2^nd Edition, Sebastopol, CA: O’Reilly Media Inc
Fisher, R. A. (1956). Statistical Methods and Scientific Inference, New York: Hafner Publishing Company.
Hogg, R. V.; McKean, J. W. & Craig, A. T. (2013). Introduction to Mathematical Statistics, 7^th Edition, New Delhi: Pearson India.
IBM SPSS Statistics. (2020). IBM Corporation.
Levin, R. I.; Rubin, D. S; Siddiqui, M. H. & Rastogi, S. (2017). Statistics for Management, 8^th Edition, New Delhi: Pearson India.

If you want to get a detailed understanding of Hypothesis testing, you can take up this hypothesis testing in machine learning course. This course will also provide you with a certificate at the end of the course.

If you want to learn more about R programming and other concepts of Business Analytics or Data Science, sign up for Great Learning’s PG program in Data Science and Business Analytics.