- What is Multiclass Classification?
- Which classifiers do we use in multiclass classification? When do we use them?
- What is Entropy?
- What is Gini Index?
- Confusion Matrix in Multi-class Classification
- Multiclass Vs Multi-label
Contributed by: Ayushi Jain
LinkedIn Profile: https://www.linkedin.com/in/ayushi-jain-541047131/
We have heard about classification and regression techniques in machine learning. We know that these two techniques work on different algorithms for discrete and continuous data respectively. In this article, we will learn more about classification. If we dig deeper into classification, we deal with two types of target variables, binary class, and multi-class target variables.
Binary, as the name suggests, has two categories in the dependent column. Multiclass refers to columns with more than two categories in it.
You will get answers to all the questions that might cross your mind while reading this article, such as:
- What is multiclass classification?
- Which classifiers do we use in multiclass classification?
- How and when do we use these classifiers?
- Is multiclass and multi-label classification similar?
What is multiclass classification?
Classification means categorizing data and forming groups based on the similarities. In a dataset, the independent variables or features play a vital role in classifying our data. When we talk about multiclass classification, we have more than two classes in our dependent or target variable, as can be seen in Fig.1:
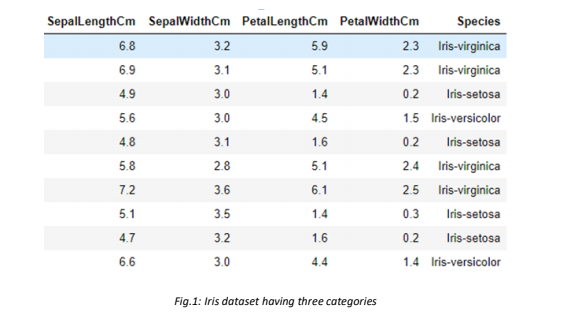
The above picture is taken from the Iris dataset which depicts that the target variable has three categories i.e., Virginica, setosa, and Versicolor, which are three species of Iris plant. We might use this dataset later, as an example of a conceptual understanding of multiclass classification.
Which classifiers do we use in multiclass classification? When do we use them?
We use many algorithms such as Naïve Bayes, Decision trees, SVM, Random forest classifier, KNN, and logistic regression for classification. But we might learn about only a few of them here because our motive is to understand multiclass classification. So, using a few algorithms we will try to cover almost all the relevant concepts related to multiclass classification.
Naive Bayes
Naive Bayes is a parametric algorithm which means it requires a fixed set of parameters or assumptions to simplify the machine’s learning process. In parametric algorithms, the number of parameters used is independent of the size of training data.
Naïve Bayes Assumption:
- It assumes that features of a dataset are completely independent of each other. But it is generally not true that is why we also call it a ‘naïve’ algorithm.
It is a classification model based on conditional probability and uses Bayes theorem to predict the class of unknown datasets. This model is mostly used for large datasets as it is easy to build and is fast for both training and making predictions. Moreover, without hyperparameter tuning, it can give you better results as compared to other algorithms.
Naïve Bayes can also be an extremely good text classifier as it performs well, such as in the spam ham dataset.
Bayes theorem is stated as-
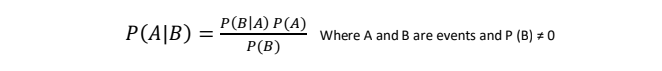
- By P (A|B), we are trying to find the probability of event A given that event B is true. It is also known as posterior probability.
- Event B is known as evidence.
- P (A) is called priori of A which means it is probability of event before evidence is seen.
- P (B|A) is known as conditional probability or likelihood.
Note: Naïve Bayes’ is linear classifier which might not be suitable to classes that are not linearly separated in a dataset. Let us look at the figure below:
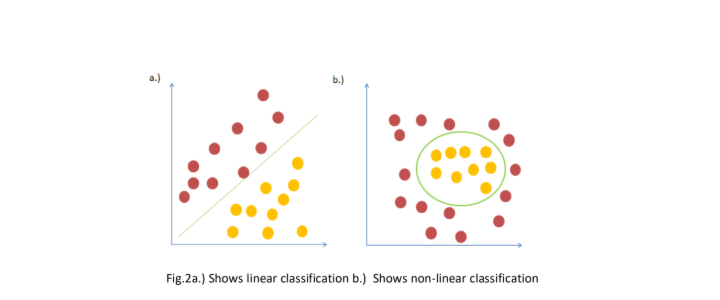
As can be seen in Fig.2b, Classifiers such as KNN can be used for non-linear classification instead of Naïve Bayes classifier.
KNN (K-nearest neighbours)
KNN is a supervised machine learning algorithm that can be used to solve both classification and regression problems. It is one of the simplest algorithms yet powerful one. It does not learn a discriminative function from the training data but memorizes the training data instead. Due to the very same reason, it is also known as a lazy algorithm.
How it works?
The K-nearest neighbor algorithm forms a majority vote between the K most similar instances, and it uses a distance metric between the two data points for defining them as similar. Most popular choice is Euclidean distance which is written as:
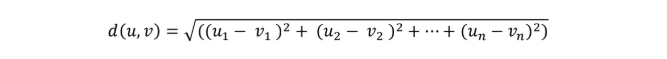
K in KNN is the hyperparameter that can be chosen by us to get the best possible fit for the dataset. If we keep the smallest value for K, i.e. K=1, then the model will show low bias, but high variance because our model will be overfitted in this case. Whereas, a larger value for K, lets suppose k=10, will surely smoothen our decision boundary, which means low variance but high bias. So we always go for a trade-off between the bias and variance, known as bias-variance trade-off.
Let us understand more about it by looking at its advantages and disadvantages:
Advantages-
- KNN makes no assumptions about the distribution of classes i.e. it is a non-parametric classifier
- It is one of the methods that can be widely used in multiclass classification
- It does not get impacted by the outliers
- This classifier is easy to use and implement
Disadvantages-
- K value is difficult to find as it must work well with test data also, not only with the training data
- It is a lazy algorithm as it does not make any models
- It is computationally extensive because it measures distance with each data point
Decision Trees
As the name suggests, the decision tree is a tree-like structure of decisions made based on some conditional statements. This is one of the most used supervised learning methods in classification problems because of their high accuracy, stability, and easy interpretation. They can map linear as well as non-linear relationships in a good way.
Let us look at the figure below, Fig.3, where we have used adult census income dataset with two independent variables and one dependent variable. Our target or dependent variable is income, which has binary classes i.e, <=50K or >50K.
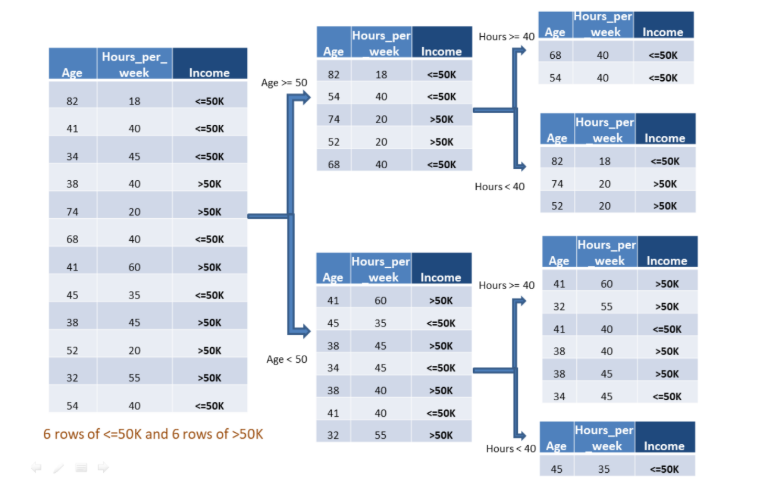
We can see that the algorithm works based on some conditions, such as Age <50 and Hours>=40, to further split into two buckets for reaching towards homogeneity. Similarly, we can move ahead for multiclass classification problem datasets, such as Iris data.
Now a question arises in our mind. How should we decide which column to take first and what is the threshold for splitting? For splitting a node and deciding threshold for splitting, we use entropy or Gini index as measures of impurity of a node. We aim to maximize the purity or homogeneity on each split, as we saw in Fig.2.
What is Entropy?
Entropy or Shannon entropy is the measure of uncertainty, which has a similar sense as in thermodynamics. By entropy, we talk about a lack of information. To understand better, let us suppose we have a bag full of red and green balls.
Scenario1: 5 red balls and 5 green balls.
If you are asked to take one ball out of it then what is the probability that the ball will be green colour ball?
Here we all know there will have 50% chances that the ball we pick will be green.
Scenario2: 1 red and 9 green balls
Here the chances of red ball are minimum and we are certain enough that the ball we pick will be green because of its 9/10 probability.
Scenario3: 0 red and 10 green balls
In this case, we are very certain that the ball we pick is of green colour.
In the second and third scenario, there is high certainty of green ball in our first pick or we can say there is less entropy. But in the first scenario there is high uncertainty or high entropy.
Entropy ∝ Uncertainty
Formula for entropy:
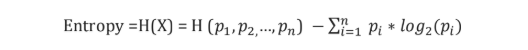
Where p(i) is probability of an element/class ‘i’ in the data
After finding entropy we find Information gain which is written as below:
What is Gini Index?
Gini is another useful metric to decide splitting in decision trees.
Gini Index formula:
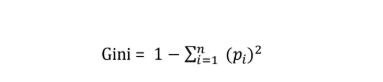
Where p(i) is probability of an element/class ‘i’ in the data.
We have always seen logistic regression is a supervised classification algorithm being used in binary classification problems. But here, we will learn how we can extend this algorithm for classifying multiclass data. In binary, we have 0 or 1 as our classes, and the threshold for a balanced binary classification dataset is generally 0.5. Whereas, in multiclass, there can be 3 balanced classes for which we require 2 threshold values which can be, 0.33 and 0.66. But a question arises, by using what method do we calculate threshold and approach multiclass classification? So let’s first see a general formula that we use for the logistic regression curve:
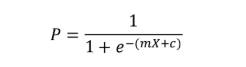
Where P is the probability of the event occurring and the above equation derives from here:
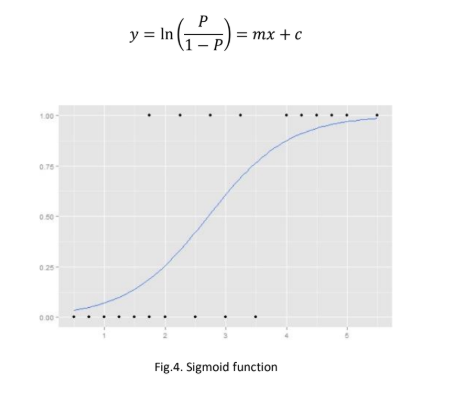
There are two ways to approach this kind of a problem. They are explained as below:
One vs. Rest (OvR)– Here, one class is considered as positive, and rest all are taken as negatives, and then we generate n-classifiers. Let us suppose there are 3 classes in a dataset, therefore in this approach, it trains 3-classifiers by taking one class at a time as positive and rest two classes as negative. Now, each classifier predicts the probability of a particular class and the class with the highest probability is the answer.
One vs. One (OvO)– In this approach, n ∗ (n − 1)⁄2 binary classifier models are generated. Here each classifier predicts one class label. Once we input test data to the classifier, the class which has been predicted the most is chosen as the answer.
Confusion Matrix in Multi-class Classification
A confusion matrix is table which is used in every classification problem to describe the performance of a model on a test data.
As we know about confusion matrix in binary classification, in multiclass classification also we can find precision and recall accuracy.
Let’s take an example to have a better idea about confusion matrix in multiclass classification using Iris dataset which we have already seen above in this article.
Finding precision and recall from above Table.1:
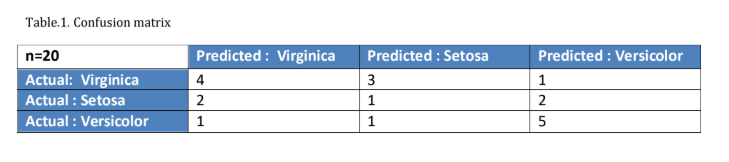
Precision for Virginica class is the number of correctly predicted virginica species out of all the predicted virginica species, which is 4/7 = 57.1%. This means that only 4/7 of the species that our predictor classifies as Virginica are actually virginica. Similarly, we can find for other species i.e. for Setosa and Versicolor, precision is 20% and 62.5% respectively.
Whereas, Recall for Virginica class is the number of correctly predicted virginica species out of actual virginica species, which is 50%. This means that our classifier classified half of the virginica species as virginica. Similarly, we can find for other species i.e. for Setosa and Versicolor, recall is 20% and 71.4% respectively.
Multiclass Vs Multi-label
People often get confused between multiclass and multi-label classification. But these two terms are very different and cannot be used interchangeably. We have already understood what multiclass is all about. Let’s discuss in brief how multi-label is different from multiclass.
Multi-label refers to a data point that may belong to more than one class. For example, you wish to watch a movie with your friends but you have a different choice of genres that you all enjoy. Some of your friends like comedy and others are more into action and thrill. Therefore, you search for a movie that fulfills both the requirements and here, your movie is supposed to have multiple labels. Whereas, in multiclass or binary classification, your data point can belong to only a single class. Some more examples of the multi-label dataset could be protein classification in the human body, or music categorization according to genres. It can also one of the concepts highly used in photo classification.
I hope this article has provided you with some fair conceptual knowledge. Don’t stop here, remember that there are many more ways to classify your data. All that is important is how you polish your basics to create and implement more algorithms. Let us conclude by looking at what Professor Pedro Domingos said-
“Machine learning will not single-handedly determine the future, any more than any other technology; it’s what we decide to do with it that counts, and now you have the tools to decide.”
If you found this helpful and wish to learn more such concepts, join Great Learning Academy’s free courses today!
